-
Looking for HSC notes and resources? Check out our Notes & Resources page
HSC 2015 MX1 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Re: HSC 2015 3U Marathon
 and then manipulate.$)
Re: HSC 2015 3U Marathon
InteGrand have you got any tips for projectile motion in regards to how I should be approaching them (And if possible could you please post all necessary equations in case I have missed anything) ?
They tend to be in tiered questions (i.e. a, b, c, etc.) and the one's that say "show that" (I'm not talking about the easy "show that" ones like deriving the horizontal and vertical displacement equations) give me an idea of what manipulations are necessary, etc. whilst others can be really dodgy and I find it difficult to begin the question :/
InteGrand have you got any tips for projectile motion in regards to how I should be approaching them (And if possible could you please post all necessary equations in case I have missed anything) ?
They tend to be in tiered questions (i.e. a, b, c, etc.) and the one's that say "show that" (I'm not talking about the easy "show that" ones like deriving the horizontal and vertical displacement equations) give me an idea of what manipulations are necessary, etc. whilst others can be really dodgy and I find it difficult to begin the question :/
davidgoes4wce
Well-Known Member
Re: HSC 2015 3U Marathon
Is that formula a thing we need to remember? I for one using all my textbooks have not seen that before. (My formula book is the Warwick Marlin book .)
Is that formula a thing we need to remember? I for one using all my textbooks have not seen that before. (My formula book is the Warwick Marlin book .)
Re: HSC 2015 3U Marathon
Well it's good to keep it in mind, but you'll usually be given it or asked to derive it if you need it. And it's given to you in the question you posted.Is that formula a thing we need to remember? I for one using all my textbooks have not seen that before. (My formula book is the Warwick Marlin book .)
davidgoes4wce
Well-Known Member
Re: HSC 2015 3U Marathon
AS much as a challenging subject this is, I love it. There is a sense of satisfaction once you do more and more of these questions. (and start getting a few right)
AS much as a challenging subject this is, I love it. There is a sense of satisfaction once you do more and more of these questions. (and start getting a few right)
davidgoes4wce
Well-Known Member
Re: HSC 2015 3U Marathon
I'm putting all my focus on the 3 Unit Maths this year and next year I'll do the 4 Unit maths.
I'm putting all my focus on the 3 Unit Maths this year and next year I'll do the 4 Unit maths.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 3U Marathon
Three men Bill, Garry and Jason observe a vertical tower. Bill stands du North of the tower, and sees its top at an angle of elevation of A. Garry stands due East of the tower, and sees its top at an angle of elevation of B. Jason stands on a line from Bill to Garry, exactly half way between them.
If Jason observes the top of the tower at an angle of elevation of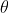
Show that
Three men Bill, Garry and Jason observe a vertical tower. Bill stands du North of the tower, and sees its top at an angle of elevation of A. Garry stands due East of the tower, and sees its top at an angle of elevation of B. Jason stands on a line from Bill to Garry, exactly half way between them.
If Jason observes the top of the tower at an angle of elevation of
Show that
Re: HSC 2015 3U Marathon
|=\sqrt{\dot{x}(t)^2 + \dot{y}(t)^2}) and that the angle the projectile is making with the horizontal at any time is given by
and that the angle the projectile is making with the horizontal at any time is given by  )= \frac{\dot{y}(t)}{\dot{x}(t)}) .
.
Another thing to keep in mind is that the horizontal range is maximised when the angle of projection α is 45º (so tan(α) = 1). This is quite easy to forget sometimes but I remember it being useful for a projectile Q in a past HSC (can't remember which year or the exact Q).
I guess most of the harder 'show that' Q's mostly require practice to improve (seeing many different Q's and reflecting on their solutions etc., since there are quite a variety of Q's that can be asked in the harder range for projectiles, but certain solution techniques may manifest themselves in other Q's). Often they're Q's like 'show that if the ball passes through a hole, then ...', or something like that. So for these types of Q's, you should think about what it means mathematically for the ball to pass through the hole (e.g. it might mean: when x = a, the height of the ball is between b and c, i.e. b < y(a) < c, where y(x) is the trajectory as a function of x (which you will probably get asked to derive beforehand). Then from the inequality b < y(a) < c, manipulating from here may lead to the desired result), and then work from there.
You can try Q7 from the 1995 HSC 3U paper for practice, probably one of the hardest projectile motion Q's in HSC 3U from the past 20 years (took up all of Q7 there), or just post Q's on here : http://www.boardofstudies.nsw.edu.au/hsc_exams/hsc2000exams/hsc00_maths/95MAT3U.PDF.
: http://www.boardofstudies.nsw.edu.au/hsc_exams/hsc2000exams/hsc00_maths/95MAT3U.PDF.
Some useful equations that are not always emphasised are that the net speed of the ball at any time isInteGrand have you got any tips for projectile motion in regards to how I should be approaching them (And if possible could you please post all necessary equations in case I have missed anything) ?
They tend to be in tiered questions (i.e. a, b, c, etc.) and the one's that say "show that" (I'm not talking about the easy "show that" ones like deriving the horizontal and vertical displacement equations) give me an idea of what manipulations are necessary, etc. whilst others can be really dodgy and I find it difficult to begin the question :/
Another thing to keep in mind is that the horizontal range is maximised when the angle of projection α is 45º (so tan(α) = 1). This is quite easy to forget sometimes but I remember it being useful for a projectile Q in a past HSC (can't remember which year or the exact Q).
I guess most of the harder 'show that' Q's mostly require practice to improve (seeing many different Q's and reflecting on their solutions etc., since there are quite a variety of Q's that can be asked in the harder range for projectiles, but certain solution techniques may manifest themselves in other Q's). Often they're Q's like 'show that if the ball passes through a hole, then ...', or something like that. So for these types of Q's, you should think about what it means mathematically for the ball to pass through the hole (e.g. it might mean: when x = a, the height of the ball is between b and c, i.e. b < y(a) < c, where y(x) is the trajectory as a function of x (which you will probably get asked to derive beforehand). Then from the inequality b < y(a) < c, manipulating from here may lead to the desired result), and then work from there.
You can try Q7 from the 1995 HSC 3U paper for practice, probably one of the hardest projectile motion Q's in HSC 3U from the past 20 years (took up all of Q7 there), or just post Q's on here
Last edited:
davidgoes4wce
Well-Known Member
davidgoes4wce
Well-Known Member
Re: HSC 2015 3U Marathon
Also the 2nd line on the R.H.S should be tan^(-1)=1/x
Also the 2nd line on the R.H.S should be tan^(-1)=1/x
Re: HSC 2015 3U Marathon

That was a pretty good question
I was surprised that they required you to use the 2 unit formula of l = r(theta)
I got every part but was unsure about my reasoning for the first part. They say that it is tangential at P and Q, so would it suffice to say that since its a right angle triangle you can apply Pythagoras' Theorem?
Thanks heapsSome useful equations that are not always emphasised are that the net speed of the ball at any time isand that the angle the projectile is making with the horizontal at any time is given by
.
Another thing to keep in mind is that the horizontal range is maximised when the angle of projection α is 45º (so tan(α) = 1). This is quite easy to forget sometimes but I remember it being useful for a projectile Q in a past HSC (can't remember which year or the exact Q).
I guess most of the harder 'show that' Q's mostly require practice to improve (seeing many different Q's and reflecting on their solutions etc., since there are quite a variety of Q's that can be asked in the harder range for projectiles, but certain solution techniques may manifest themselves in other Q's). Often they're Q's like 'show that if the ball passes through a hole, then ...', or something like that. So for these types of Q's, you should think about what it means mathematically for the ball to pass through the hole (e.g. it might mean: when x = a, the height of the ball is between b and c, i.e. b < y(a) < c, where y(x) is the trajectory as a function of x (which you will probably get asked to derive beforehand). Then from the inequality b < y(a) < c, manipulating from here may lead to the desired result), and then work from there.
You can try Q7 from the 1995 HSC 3U paper for practice, probably one of the hardest projectile motion Q's in HSC 3U from the past 20 years (took up all of Q7 there), or just post Q's on here: http://www.boardofstudies.nsw.edu.au/hsc_exams/hsc2000exams/hsc00_maths/95MAT3U.PDF.
That was a pretty good question
I was surprised that they required you to use the 2 unit formula of l = r(theta)
I got every part but was unsure about my reasoning for the first part. They say that it is tangential at P and Q, so would it suffice to say that since its a right angle triangle you can apply Pythagoras' Theorem?
Re: HSC 2015 3U Marathon
 in that one. Edit: Are you talking about Q 6(b) there? (I meant Q7 for the projectile Q in that link.)
in that one. Edit: Are you talking about Q 6(b) there? (I meant Q7 for the projectile Q in that link.)
Which Q are you talking about? Not the one in the link (1995 HSC) right? Since there's no involvement ofThanks heaps
That was a pretty good question
I was surprised that they required you to use the 2 unit formula of l = r(theta)
I got every part but was unsure about my reasoning for the first part. They say that it is tangential at P and Q, so would it suffice to say that since its a right angle triangle you can apply Pythagoras' Theorem?
Last edited:
Re: HSC 2015 3U Marathon
Yeah, except not Pythagoras' Theorem, just simple right-angled trigonometry (i.e. cosine(angle) = adjacent/hypotenuse).I got every part but was unsure about my reasoning for the first part. They say that it is tangential at P and Q, so would it suffice to say that since its a right angle triangle you can apply Pythagoras' Theorem?
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 3U Marathon
BUMPThree men Bill, Garry and Jason observe a vertical tower. Bill stands du North of the tower, and sees its top at an angle of elevation of A. Garry stands due East of the tower, and sees its top at an angle of elevation of B. Jason stands on a line from Bill to Garry, exactly half way between them.
If Jason observes the top of the tower at an angle of elevation of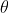
Show that
Re: HSC 2015 3U Marathon
*sighs* Apologies for the hard derping I'm usually not the one to stay up at a time like this
Oh sht yeah I meant trigYeah, except not Pythagoras' Theorem, just simple right-angled trigonometry (i.e. cosine(angle) = adjacent/hypotenuse).
*sighs* Apologies for the hard derping I'm usually not the one to stay up at a time like this
Re: HSC 2015 3U Marathon
l = 3 ( (pi) - (theta))
From cos(theta) = 3 / x ------> theta = inverse[cos] 3 / x
Therefore
l = 3 ( (pi) - inverse[cos] 3 / x)
Yeah I double derped that's actually question 6
It isn't even projectile LOL
I'm gonna go to bed and do it tomorrow morning
Good Night!
Yeah I used it in 7Which Q are you talking about? Not the one in the link (1995 HSC) right? Since there's no involvement ofin that one. Edit: Are you talking about Q 6(b) there? (I meant Q7 for the projectile Q in that link.)
l = 3 ( (pi) - (theta))
From cos(theta) = 3 / x ------> theta = inverse[cos] 3 / x
Therefore
l = 3 ( (pi) - inverse[cos] 3 / x)
Yeah I double derped that's actually question 6
It isn't even projectile LOL
I'm gonna go to bed and do it tomorrow morning
Good Night!
davidgoes4wce
Well-Known Member
davidgoes4wce
Well-Known Member
Re: HSC 2015 3U Marathon
In terms of MCQ, the choice I would go for is between the interval 1/4 < x < 1/2. But we would have to obtain the step up above using a calculator.
In terms of MCQ, the choice I would go for is between the interval 1/4 < x < 1/2. But we would have to obtain the step up above using a calculator.
Re: HSC 2015 3U Marathon
, we have that $x=\tan \frac{\pi}{8}$ (this is obtained by doing everything in terms of $\tan^{-1}x$ instead of $\tan^{-1}\frac{1}{x}$). Now draw a diagram of the tan function $y=\tan t$ over the interval $\left[0,\frac{\pi}{4}\right]$. We know that $\tan(0)=0$ and $\tan \frac{\pi}{4}=1$, and that the function is increasing and concave up here.$)
 connecting the points $(0,0)$ and $\left(\frac{\pi}{4},1\right)$ on the graph of $y=\tan t$ is entirely above the curve in the interval $\left(0,\frac{\pi}{4}\right)$. In particular, the midpoint of this segment is above the curve. Then since the midpoint of the secant is the point $\left(\frac{\pi}{8},\frac{1}{2} \right)$, and the curve here has the value $x$ (since $x=\tan \frac{\pi}{8}$), we have $x<\frac{1}{2}$.$)
$ is entirely below the curve in the interval $\left(0,\frac{\pi}{4}\right)$. Since the tangent line is $y=t$ (which you can show via calculus), it follows that the $y$-value of the tangent line at $t=\frac{\pi}{8}$ (which is $\frac{\pi}{8}$) is below that of the curve (and the curve's value here is $\tan\frac{\pi}{8}=x$). Therefore, $\frac{\pi}{8}<x$. (All this should be relatively clear from a sketch.)$)
.$)
In terms of MCQ, the choice I would go for is between the interval 1/4 < x < 1/2. But we would have to obtain the step up above using a calculator.
Last edited:
- Status
- Not open for further replies.


