Obviously, a proof by contradiction seems like the correct approach.
Choose a point in the plane, and label it as A_0. From the questions conditions, namely the fact that not all lines can intersect at a single point implies that there are in fact at least three distinct intersection points. Of all triangles whose vertices are such intersection points, consider those with minimal area; and of all these triangles, consider one whose centroid is farthest from A_0.
Suppose that this triangle has vertices P, Q, and R. Because these points are have three or more lines going through them, they must lie also on the sides of a bigger triangle. This new, larger triangle is separated into four triangles by the lines PQ, QR, and RP — namely, triangle PQR is surrounded by three outer triangles.
One can easily show that the PQR's area is >= the minimum of the areas of the other three triangles,
with equality if and only if triangle PQR is the medial triangle of the larger triangle whose sides P,Q, and R lie on. Indeed, equality must hold because of the minimal definition of triangle PQR. Hence, each of the outer triangles is formed by the given lines and has the same area as triangle PQR; but one of the four triangles have centroids further from A_0 than
the centroid of triangle PQR, a contradiction since we defined PQR to be the triangle whose triangle has minimal distance from A_0.
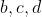 allowed to be non-real complex numbers? Do you mean
allowed to be non-real complex numbers? Do you mean 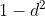 , or
, or 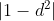 ? And is
? And is 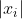 the root, or is it
the root, or is it 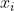 ? It is possible to have all roots have modulus less than 1 and have
? It is possible to have all roots have modulus less than 1 and have 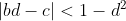 be unsatisfied, e.g.
be unsatisfied, e.g.  = x^3 - \frac{1}{8}\mathrm{cis}(\theta)) for some real
for some real 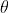 such that
such that  \right)^2) is not real (clearly such
is not real (clearly such 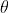 exists). In this case,
exists). In this case, 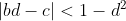 does not make sense since
does not make sense since 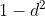 is not real.
is not real.