-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
How do you determine the graph shape for complex number locuses? (1 Viewer)
- Thread starter sadpwner
- Start date
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
The ones involving just distances to two points that are good to recognise:
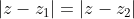
(the line that bisects z1z2).
)
(the circle with diameter given by the line segment joining the internal and external points of k:1 division).
)
(the ellipse with focii at z1 and z2 with semimajor axis length k/2).
)
(the hyperbola with focii at z1 and z2 with distance between branches k/2).
You should also recognise the ones comparing distance to a point and distance to a line, like
\quad (e>0))
(the conic with eccentricity e that has a focus at z1 and the x-axis as its corresponding directrix.)
(the line that bisects z1z2).
(the circle with diameter given by the line segment joining the internal and external points of k:1 division).
(the ellipse with focii at z1 and z2 with semimajor axis length k/2).
(the hyperbola with focii at z1 and z2 with distance between branches k/2).
You should also recognise the ones comparing distance to a point and distance to a line, like
(the conic with eccentricity e that has a focus at z1 and the x-axis as its corresponding directrix.)
For your 3rd example, I don't think k>0 is sufficiently restrictive in order to get an ellipse.The ones involving just distances to two points that are good to recognise:
(the line that bisects z1z2).
(the circle with diameter given by the line segment joining the internal and external points of k:1 division).
(the ellipse with focii at z1 and z2 with semimajor axis length k/2).
(the hyperbola with focii at z1 and z2 with distance between branches k/2).
You should also recognise the ones comparing distance to a point and distance to a line, like
(the conic with eccentricity e that has a focus at z1 and the x-axis as its corresponding directrix.)
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Ah yes, neither for the hyperbola.For your 3rd example, I don't think k>0 is sufficiently restrictive in order to get an ellipse.
We require k > |z1-z2| for the ellipse and k < |z1-z2| for the hyperbola to avoid degeneracy.
And ... if you'll allow me to be even more picky (for the sake of OP, not you):Ah yes, neither for the hyperbola.
We require k > |z1-z2| for the ellipse and k < |z1-z2| for the hyperbola to avoid degeneracy.
In the 2nd we need k not equal to 1 (if we really want a circle).
And for the last one, you probably want an absolute value around the Im(z), unless you specify Im(z_1) > 0 for an ellipse, or unless you want only one branch of a hyperbola.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Yep, by all means.And ... if you'll allow me to be even more picky (for the sake of OP, not you):
In the 2nd we need k not equal to 1 (if we really want a circle).
And for the last one, you probably want an absolute value around the Im(z), unless you specify Im(z_1) > 0 for an ellipse, or unless you want only one branch of a hyperbola.
Cheers, will amend a little later.

