Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
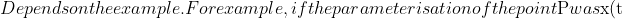=t^2$ and $y(t)=2$, $t\in \mathbb{R}$, then since the range of the function $x(t) = t^2$ is the set of non-negative real numbers, the locus of $P$ will be the portion of the line $y=2$ where $x\geq 0$ (in other words, the right-half of the line, including the point $(0,2)$. In fact, $P$ would trace out this portion of the line twice as $t$ varies through the reals.$)
how would you check for restrictions??
how would you check for restrictions??
P (2ap, ap^2) and Q (2aq,aq^2) are points on x^2 = 4ay , and he chord PQ subtends a right angle at the vertex O.
Show that pq = -4
It's probably really simple but I can't seem to work it out!
Two points P and Q where p > q, move along the parabola x^2 = 4ay . At all times the x cordinates of P and Q differ by 2a.
Find the midpoint of the chord PQ.
M ( a(p + q), 1/2 a(p^2 + q^2))
Now how do i find the cartesian equation of its locus.
I have put
x = a ( p + q)
y = 1/2 a (p^2 + q^2)
But am stumped on where to go.
determine the arcs specified by the following eqn. Sketch each one, showing the centre and radius of the associated circle.
arg ( z - 1 + i) / (z - 1 - i ) = pi/2
So i know it a circle. there are endpoints at (1, -1 ) and ( 1, 1) and that there are not included , hollow dot.
The angle between these two vectors when they meet is pi /2 .
The answers say it is a right hand side semicircle. Why is it a semicircle and not a full circle??
how do you sketch y = -1/2 ( x^2 + 1) ??
Since |a/b|=|a|/|b| (in words, the modulus of the quotient is the quotient of the moduli)How do you shade the region defined by the inequality | (z + 1)/ (z - i ) | greater than or equal to 1
Am i right in saying:
1) let z = x + iy
2) rationalise the denominator
3) then get it in the form of x + iy
4) Use sqrt x^2 + y^2
5)get a circle
Is this correct. Seems to long of a method for this question. Is there a faster and shorter way I don't know of??
How do you shade the region defined by the inequality | (z + 1)/ (z - i ) | greater than or equal to 1
Am i right in saying:
1) let z = x + iy
2) rationalise the denominator
3) then get it in the form of x + iy
4) Use sqrt x^2 + y^2
5)get a circle
Is this correct. Seems to long of a method for this question. Is there a faster and shorter way I don't know of??
I have sketched the locus of arg( z - i ) = pi/3
Now how do I find the cartesian equation of the locus, stating any restrictions on the domain.
Unsure how to get the equation. Do i sub in x + iy for z ??
For Sketch the locus represented by the equation |z^2 - z -2 | = | z + 1|
Do i just use z = x + iy and simplify
I am half way through this method and its a huge mess of expansion.
I'm not the best at maths but could i get help on Chapter 10: The Geometry of the Derivative 10A: Increasing, Decreasing and Stationary at a Point (Page 359, Exercise 10A, Question 2)
2.a) Show that y = -5x + 2 is decreasing for all x
b) Show that y = x + 7 is increasing for all x
There arent any answers to ths question in the textbook. Any help would be much appreciated ^^
