HSC 2016 MX1 Marathon (archive) (1 Viewer)

InteGrand · Feb 2, 2016

Re: Flop math question thread

Flop21 said:
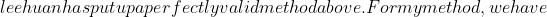
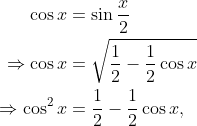
I keep getting a power to 3, instead of 2 to solve for quadratic.

$\noindent leehuan has put up a perfectly valid method above. For my method, we have$

$$\begin{align*}\cos x &=\sin \frac{x}{2} \\ \Rightarrow \cos x &= \sqrt{\frac{1}{2} -\frac{1}{2}\cos x}\\ \Rightarrow \cos^2 x &=\frac{1}{2}-\frac{1}{2}\cos x, \end{align*}$

$\noindent which is a quadratic in $\cos x$.$

davidgoes4wce · Feb 2, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
$\noindent There is a room with $k$ people in it. Assume birthdays are random, leap years do not exist, and that twins and other instances of multi-births do not exist. What is the least possible $k$ such that the probability of two people sharing the same birthday exceeds 99.95$\%$?$

Consider an example where there are 25 people in a room, that gives us 300 pairs.

davidgoes4wce · Feb 2, 2016

Re: HSC 2016 3U Marathon

I used the example with a probability value of 0.9975 when it should have been 0.9995, that changes the answer fairly significantly.

InteGrand · Feb 2, 2016

Re: HSC 2016 3U Marathon

davidgoes4wce said:
I used the example with a probability value of 0.9975 when it should have been 0.9995, that changes the answer fairly significantly.

Your method wasn't actually quite correct. This is because the events of pairs having different birthdays are not independent events, so we can't just multiply the probabilities like that. If we could just multiply them like that, we'd always have a non-zero probability of having no pairs with same birthday (just like there's always a non-zero probability of getting no tails from a set of coin tosses). But clearly if we had 366 people in the room, we always will have a pair with same birthdays, by the pigeonhole principle.

Paradoxica · Feb 2, 2016

Re: HSC 2016 3U Marathon

$\noindent a) ${-1,x,x^3}$ is an arithmetic progression.$\\$Find $x$, given $-1$ trivially satisfies the above sequence.$ \\ \phi $ is the positive solution to the above equation.$ \\ $b) Show by induction or other means that $\phi^{2n}+\phi^{-2n}$ is an integer.$ \\ $c) Similarly, show $\phi^{2n+1}-\phi^{-(2n+1)}$ is an integer.$

Drsoccerball · Feb 3, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
$\noindent a) ${-1,x,x^3}$ is an arithmetic progression.$\\$Find $x$, given $\phi$, the golden ratio is a root.$ \\ $b) Show by induction or other means that $\phi^{2n}+\phi^{-2n}$ is an integer.$ \\ $c) Similarly, show $\phi^{2n+1}-\phi^{-(2n+1)}$ is an integer.$

$Hint: Take note that $ \phi ^{2n} +\phi ^{-2n} = (1+\phi)^n + \frac{1}{(1+\phi) ^n} $ Use induction and double assumption.$

Drsoccerball · Feb 3, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
$\noindent There is a room with $k$ people in it. Assume birthdays are random, leap years do not exist, and that twins and other instances of multi-births do not exist. What is the least possible $k$ such that the probability of two people sharing the same birthday exceeds 99.95$\%$?$

I think people should take note that $2 \leq k \leq 366$

Paradoxica · Feb 3, 2016

Re: HSC 2016 3U Marathon

Drsoccerball said:
$Hint: Take note that $ \phi ^{2n} +\phi ^{-2n} = (1+\phi)^n + \frac{1}{(1+\phi) ^n} $ Use induction and double assumption.$

Stop giving hints.

leehuan · Feb 3, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
Stop giving hints.

Well I haven't done enough questions like this so whilst I considered the relationship between the golden ratio and it's square both having √5/2 I overlooked the rewriting of the expression

Paradoxica · Feb 3, 2016

Re: HSC 2016 3U Marathon

leehuan said:
Well I haven't done enough questions like this so whilst I considered the relationship between the golden ratio and it's square both having √5/2 I overlooked the rewriting of the expression

I expect everyone to know the quadratic relation of the golden ratio. I have few standards, but assumed knowledge is one of them.

Drsoccerball · Feb 3, 2016

Re: HSC 2016 3U Marathon

$\phi = \sqrt{1+\sqrt{1+\sqrt{1+...}}$

$\int{\sqrt{x+\sqrt{x+\sqrt{x+...}}}dx $ I learnt golden ratio from questions like this. $$

leehuan · Feb 3, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
I expect everyone to know the quadratic relation of the golden ratio. I have few standards, but assumed knowledge is one of them.

(3+√5)/2 = 1 + (1+√5)/2 went over my head because I forgot the exact thing Drsoccerball mentioned just now

That being said however, whilst it may have been bad that I forgot it, I hope you're not gonna say that to every 3U student out there.

Drsoccerball · Feb 3, 2016

Re: HSC 2016 3U Marathon

leehuan said:
(3+√5)/2 = 1 + (1+√5)/2 went over my head because I forgot the exact thing Drsoccerball mentioned just now

That being said however, whilst it may have been bad that I forgot it, I hope you're not gonna say that to every 3U student out there.

Golden ratio shouldn't even be known by a good extension 2 student.

InteGrand · Feb 3, 2016

Re: HSC 2016 3U Marathon

$\noindent Since knowledge of the golden ratio's definition isn't expected in the HSC, I'll provide it here: it's the positive root of the quadratic equation $x^2-x-1=0$.$

leehuan · Feb 3, 2016

Re: HSC 2016 3U Marathon

InteGrand said:
$\noindent Since knowledge of the golden ratio's definition isn't expected in the HSC, I'll provide it here: it's the positive root of the quadratic equation $x^2-x-1=0$.$

Part (a) was easy because I remembered this

Drsoccerball · Feb 3, 2016

Re: HSC 2016 3U Marathon

leehuan said:
Part (a) was easy because I remembered this

$Y= \sqrt{1+\sqrt{1+\sqrt{1+...}}}$

$Y^2= 1 +Y$

$Y^2 -Y -1 =0$

leehuan · Feb 3, 2016

Re: HSC 2016 3U Marathon

Drsoccerball said:
$Y= \sqrt{1+\sqrt{1+\sqrt{1+...}}}$

$Y^2= 1 +Y$

$Y^2 -Y +1 =0$

Yes I'm well aware of the proof using that form lol. But I only remembered the quadratic equation cause I did a bit of reading on transcendental numbers the other day and noted how the golden ratio was not one.

Btw, typo, last line that should be a -1

Shuuya · Feb 3, 2016

Shuuya's endless maths questions SOS thread

I decided to stop making new threads to ask my endless maths questions, so here we are!

Inspired by leehuan's SOS thread

InteGrand · Feb 3, 2016

Re: Shuuya's endless maths questions SOS thread

Shuuya said:
I decided to stop making new threads to ask my endless maths questions, so here we are!

Inspired by leehuan's SOS thread

$\noindent i) It's an even function, so it fails the Horizontal Line Test, so is not invertible.$

$\noindent ii) Restricted to $x\geq 0$, clearly $x^2$ is monotone, so $\mathrm{e}^{x^2}$ is monotone (as the exponential function is monotone and a monotone function of a monotone function is monotone). Hence this function is invertible.$

Shuuya · Feb 3, 2016

Re: Shuuya's endless maths questions SOS thread

InteGrand said:
$\noindent i) It's an even function, so it fails the Horizontal Line Test, so is not invertible.$

$\noindent ii) Restricted to $x\geq 0$, clearly $x^2$ is monotone, so $\mathrm{e}^{x^2}$ is monotone (as the exponential function is monotone and a monotone function of a monotone function is monotone). Hence this function is invertible.$

Thanks!

HSC 2016 MX1 Marathon (archive) (1 Viewer)

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

-insert title here-

Well-Known Member

Well-Known Member

-insert title here-

Well-Known Member

-insert title here-

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)