leehuan's All-Levels-Of-Maths SOS thread (3 Viewers)

seanieg89 · Mar 12, 2016

Paradoxica said:
If a number is the root of a polynomial with algebraic co-efficients, is that number itself necessarily algebraic?

Yeah. The composition of two finite-degree field extensions is finite (degrees being multiplicative), and finite-degree extensions are algebraic.

Paradoxica · Mar 12, 2016

leehuan said:
Can someone just send me the link if they're not bothered to type it cause apparently it's a very famous result...

$\\ $Show that :$ \\ \sum_{m=1}^{99}{\frac{\sin{\left(\frac{17 m \pi}{100}\right)} \sin{\left(\frac{39 m \pi}{100}\right)}}{1+\cos{\left( \frac{m\pi}{100} \right) }}}=1037$

the obvious, messy, tedious, disgusting method of doing this is to convert the entire thing into a polynomial in terms of e^{m pi/200}

any elegant solution is beyond me.

this is probably a red herring but... 1037 = 61*17

leehuan · Mar 12, 2016

Paradoxica said:
the obvious, messy, tedious, disgusting method of doing this is to convert the entire thing into a polynomial in terms of e^{m pi/200}

any elegant solution is beyond me.

this is probably a red herring but... 1037 = 61*17

But 100-39=61
......

1037=17(100-39) how could THAT be useful...

Paradoxica · Mar 12, 2016

leehuan said:
But 100-39=61
......

1037=17(100-39) how could THAT be useful...

There's a paper which analyses similar sums, but the summand term is a quotient of perfect squares rather than different things.

Also, the general sum evaluates to Q(R-Q) where R is the final summand index.

39 = 2(17)+1 but that feels like a red herring to me.

obliviousninja · Mar 13, 2016

Prove that the half your age + 7 rule is legitimate

seanieg89 · Mar 13, 2016

leehuan said:
Can someone just send me the link if they're not bothered to type it cause apparently it's a very famous result...

$\\ $Show that :$ \\ \sum_{m=1}^{99}{\frac{\sin{\left(\frac{17 m \pi}{100}\right)} \sin{\left(\frac{39 m \pi}{100}\right)}}{1+\cos{\left( \frac{m\pi}{100} \right) }}}=1037$

Thought of a method that should work (and give us a more general formula), but it takes some doing. Will work through the details later today and post them when I do.

Nailgun · Mar 13, 2016

obliviousninja said:
Prove that the half your age + 7 rule is legitimate

Unfortunately I am not aware of a full proof, but here are some resources to help in an analysis

http://www.wolframalpha.com/input/?i=x+>=+y+/+2+++7+and+y+>=+x/2++7
https://www.researchgate.net/public..._reflect_sex_differences_in_mating_strategies
https://www.youtube.com/watch?v=7dsVYswSfow

in order of increasing usefulness

seanieg89 · Mar 13, 2016

seanieg89 said:
Thought of a method that should work (and give us a more general formula), but it takes some doing. Will work through the details later today and post them when I do.

Okay, I actually really can't be bothered to write everything up, but I will sketch each step of my computation. (This will evaluate the sum for any pair of odd integers in the numerator. Extending this to treat non-odd integers is not difficult, but it clutters the computations with (-1)^n parity factors.)

(This proof isn't very clean and there could very well be a nicer way of going about things.)

1. By using the products to differences formula, it suffices to figure out how to calculate things of the form

$J_m:=\sum_{k=1}^{99} \frac{\cos(2mk\pi/100)}{1+\cos(k\pi/100)}\quad \textrm{for }m\in\mathbb{Z}.$

2. Now a couple of trig identities, together with De'Moivres and the geometric series formula allow us to deduce the recurrence relation

$J_{m+1}-2J_m+J_{m-1}=4.$

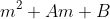
3. This is just a simple inhomogenous difference equation, In fact the LHS of the above is just a second order difference about m, which motivates the solution being quadratic. Indeed, all solutions are of the form $m^2+Am+B$ , with A and B undetermined constants. This reduces the problem to computing A and B.

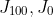
4. This can be done by explicitly computing $J_{100},J_0$ and solving the resulting simultaneous equations. To compute these two intial values of J, we have to sum 1/(1+cos(k*pi/100)). The summand is equal to 1/(2cos^2(k*pi/200)). We can treat such sums in ways analogous to the calculation in the "rigorous elementary method" section of https://en.wikipedia.org/wiki/Basel_problem.

Putting this all together completes the computation. I definitely won't write the whole working out, but I will write out my resulting formulae.

seanieg89 · Mar 13, 2016

Yep, the computations work out.

Suppose A > B are odd integers.

If you follow the above guidelines, you should obtain:

$J_0=J_{100}=3333$

$\Rightarrow J_n=2n^2-200n+3333$

$\Rightarrow \sum_{k=1}^{99}\frac{\sin(Ak\pi/100)\sin(Bk\pi/100)}{1+\cos(k\pi/100)}\\ \\ =\frac{1}{2}(J_{(A-B)/2}-J_{(A+B)/2})\\ \\=100B-AB=B(100-A).$

seanieg89 · Mar 13, 2016

(If you understand the above, then it would be good exercise for your algebra skills to generalise the result, both by replacing 100 by an arbitrary even number, and then by allowing for arbitrary parity of A,B,n.)

leehuan · Mar 14, 2016

So braindead...

$\\$Show that the line $ \textbf{x} =t \left( \begin{matrix} 2 \\ 1 \\ 3 \end{matrix} \right) $ is parallel to the plane $3x-3y-z=2$

InteGrand · Mar 14, 2016

leehuan said:
So braindead...

$\\$Show that the line$ \bf x =t \left( \begin{matrix} 2 \\ 1 \\ 3 \end{matrix} \right) $ is parallel to the plane $3x-3y-z=2$

$\noindent The given plane has a normal $\bold{n}=\left[ \begin{matrix} 3 \\ -3 \\ -1 \end{matrix} \right] $. Let $\bold{v} = \left[ \begin{matrix} 2 \\ 1 \\ 3 \end{matrix} \right]$. Then clearly $\bold{v}\cdot \bold{n} = 6-3-3 = 0$, so $\bold{v}$ is perpendicular to the normal vector $\bold{n}$, which makes it parallel to the plane. Hence the line is parallel to the plane.$

leehuan · Mar 14, 2016

InteGrand said:
$\noindent The given plane has a normal $\bold{n}=\left[ \begin{matrix} 3 \\ -3 \\ -1 \end{matrix} \right] $. Let $\bold{v} = \left[ \begin{matrix} 2 \\ 1 \\ 3 \end{matrix} \right]$. Then clearly $\bold{v}\cdot \bold{n} = 6-3-3 = 0$, so $\bold{v}$ is perpendicular to the normal vector $\bold{n}$, which makes it parallel to the plane. Hence the line is parallel to the plane.$

Sadly that doesn't fully make sense - we haven't done vectorial geometry; we're just doing an intro topic. (Though it kinda makes sense..)

We've only just defined what a plane was last lecture

InteGrand · Mar 14, 2016

leehuan said:
Sadly that doesn't fully make sense - we haven't done vectorial geometry; we're just doing an intro topic. (Though it kinda makes sense..)

We've only just defined what a plane was last lecture

$\noindent I used the following standard fact: for the plane $ax+by+cz=d$, a normal vector is $\left[ \begin{matrix} a \\ b \\ c \end{matrix} \right] $ (as well as the fact that non-zero two vectors are perpendicular iff their dot product is 0).$

InteGrand · Mar 14, 2016

seanieg89 · Mar 14, 2016

leehuan said:
So braindead...

$\\$Show that the line $ \textbf{x} =t \left( \begin{matrix} 2 \\ 1 \\ 3 \end{matrix} \right) $ is parallel to the plane $3x-3y-z=2$

A pretty ghetto way of doing it: For a point (x,y,z) on the line with parameter t, we have:

3x-3y-z=6t-3t-3t=0.

But the set of ALL (x,y,z) such that 3x-3y-z=c is a plane parallel to the given plane for any constant c (*). (Indeed that's why we evaluated this particular linear combination.)

=> the given line lies in a plane parallel to the given plane and is hence itself parallel to the given plane.

(*) To observe that the planes ax+by+cz=k are parallel as k varies, we can for instance make z the subject and interpret varying k as translating our plane in the z dimension, which intuitively preserves parallelism. (Rigorously we could also easily note that no point can lie on two such planes for different k, nonintersection being equivalent to nontrivial parallelism in this case.)

leehuan · Mar 14, 2016

I think InteGrand's added post was the thing I'm forced to use...

leehuan · Mar 15, 2016

That trigonometric sum still bugs me a tiny bit though. How do you reckon it was conjectured to begin with?

Paradoxica · Mar 15, 2016

leehuan said:
That trigonometric sum still bugs me a tiny bit though. How do you reckon it was conjectured to begin with?

I will talk about this to you on messenger.

seanieg89 · Mar 15, 2016

leehuan said:
That trigonometric sum still bugs me a tiny bit though. How do you reckon it was conjectured to begin with?

Where did you find this sum in the first place? That should provide a good clue as to the cleanest known way to compute it.

Anyway, if you find a satisfactory explanation for why it works out the way it does, please post it here.

I will probably have another think about it this evening to see if I can find a nicer way.

leehuan's All-Levels-Of-Maths SOS thread (3 Viewers)

Well-Known Member

-insert title here-

Well-Known Member

-insert title here-

(╯°□°）╯━︵ ┻━┻ - - - -

Well-Known Member

Cole World

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

-insert title here-

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 3)