leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Posting this in the 2U section as it's still within the scope of the course (even though it's just my homework).
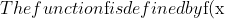={x}^{2}-4x+3$ for $0 < x \le 3$, $f(-x)=-f(x)$ for all $x$ and $f(x+6)=f(x)$ for all $x$.)
I have the graph in front of me so I can pretty much infer the answer from just that. But say I wanted to do the following question without it.
$ exist? If so, state its value.$)
Would the following method work:
}=\lim_{x\rightarrow {3}^{+}}{f^{\prime}(x)}\quad (=2)\\ \because f$ is continuous at 3.$)
_____________________________
Another question. Is this acceptable to find the limit as x approaches 3 from above (right)
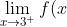}=\lim_{x\rightarrow {-3}^{+}}{f(x+6)}=\lim_{x\rightarrow {-3}^{+}}{({(x+6)}^{2}-4(x+6)+3)}=0)
I have the graph in front of me so I can pretty much infer the answer from just that. But say I wanted to do the following question without it.
Would the following method work:
_____________________________
Another question. Is this acceptable to find the limit as x approaches 3 from above (right)
Last edited:
