-
Looking for HSC notes and resources? Check out our Notes & Resources page
Higher Level Integration Marathon & Questions (3 Viewers)
- Thread starter leehuan
- Start date
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
We all know the answer is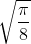
Done earlier on this thread.
We all know the answer is
KingOfActing
lukewarm mess
Re: Extracurricular Integration Marathon
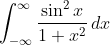
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Then why post it?Not sure if this is doable
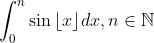
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Unsing the standard trigo-geometric summation identity for sin(x), the answer is
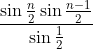
Since this is a series of rectangles across the real line, convert it into a sum.Not sure if this is doable
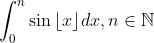
Unsing the standard trigo-geometric summation identity for sin(x), the answer is
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon

The imaginary component of the integral is absolutely convergent, and so is the Taylor expansion, so (insert reasoning here) it is valid to exchange summation, integration and complex extraction.
Take the Taylor series of ex and replace x with eix
Swap the order of integration and summation. Integrate termwise.
final answer:
π(e-1)/2
Take the Imaginary part of the following integral:
The imaginary component of the integral is absolutely convergent, and so is the Taylor expansion, so (insert reasoning here) it is valid to exchange summation, integration and complex extraction.
Take the Taylor series of ex and replace x with eix
Swap the order of integration and summation. Integrate termwise.
final answer:
π(e-1)/2
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
I don't think that integral is absolutely convergent...there might be a nice way of justifying that interchange, but its not a trivial matter.Take the Imaginary part of the following integral:
The imaginary component of the integral is absolutely convergent, and so is the Taylor expansion, so (insert reasoning here) it is valid to exchange summation, integration and complex extraction.
Take the Taylor series of ex and replace x with eix
Swap the order of integration and summation. Integrate termwise.
final answer:
π(e-1)/2
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
IDK about the justification of interchange.
The Imaginary part is absolutely convergent. The real part is divergent.I don't think that integral is absolutely convergent...there might be a nice way of justifying that interchange, but its not a trivial matter.
IDK about the justification of interchange.
Re: Extracurricular Integration Marathon
Are you absolutely (lol) sure about this?The Imaginary part is absolutely convergent. The real part is divergent.
IDK about the justification of interchange.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Dirichlet's test.Are you absolutely (lol) sure about this?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
The imaginary part of the integrand is the original integrand, which is
}\sin(\sin(x))}{x}.)
This is not absolutely convergent. We have something continuous and periodic divided by x. Upon taking absolute values, integrating this is like summing a harmonic series.
The integral converges in the sense of an improper Riemann integral because it oscillates as well as decays (things like the Dirichlet test or alternating series test pin this notion down), but its rate of decay is too slow to give us absolute convergence.
The most common ways of justifying an interchange rely on our limit function being absolutely integrable (the monotone/dominated/vitali convergence theorems), or on us having an absolutely integrable error term which we can bound and show tends to zero, so this is not as routine as you might think, even if it is probably justifiable somehow.
The imaginary part of the integrand is the original integrand, which is
This is not absolutely convergent. We have something continuous and periodic divided by x. Upon taking absolute values, integrating this is like summing a harmonic series.
The integral converges in the sense of an improper Riemann integral because it oscillates as well as decays (things like the Dirichlet test or alternating series test pin this notion down), but its rate of decay is too slow to give us absolute convergence.
The most common ways of justifying an interchange rely on our limit function being absolutely integrable (the monotone/dominated/vitali convergence theorems), or on us having an absolutely integrable error term which we can bound and show tends to zero, so this is not as routine as you might think, even if it is probably justifiable somehow.
Last edited:
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
I don't even know, Leehuan says this is from an IB textbook. Advanced much?The imaginary part of the integrand is the original integrand, which is
This is not absolutely convergent. We have something continuous and periodic divided by x. Upon taking absolute values, integrating this is like summing a harmonic series.
The integral converges in the sense of an improper Riemann integral because it oscillates as well as decays (things like the Dirichlet test or alternating series test pin this notion down), but its rate of decay is too slow to give us absolute convergence.
The most common ways of justifying an interchange rely on our limit function being absolutely integrable (the monotone/dominated convergence theorems), or on us having an absolutely integrable error term which we can bound and show tends to zero, so this is not as routine as you might think, even if it is probably justifiable somehow.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
Gotta be careful with these things, because functions/sequences that oscillate and decay but are not absolutely integrable are a common source of counterexamples to otherwise believable claims.
There has to be a less potentially dodgy way of doing it, I also thought of expanding out a series in e^(ix) to start with, but I couldn't see any way of justifying that so I left it.I don't even know, Leehuan says this is from an IB textbook. Advanced much?
Gotta be careful with these things, because functions/sequences that oscillate and decay but are not absolutely integrable are a common source of counterexamples to otherwise believable claims.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Too advanced.
Well the only other way I see is by contouring the first quadrant but like I said.There has to be a less potentially dodgy way of doing it, I also thought of expanding out a series in e^(ix) to start with, but I couldn't see any way of justifying that so I left it.
Gotta be careful with these things, because functions/sequences that oscillate and decay but are not absolutely integrable are a common source of counterexamples to otherwise believable claims.
Too advanced.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
My first thought was contouring due to the singularity but I have little experience with that.
Taylor expansion didn't occur to me until a lot later.
I only saw the imaginary extraction during an epiphany on the train last week.I don't even know at all. When I first saw this integral I had absolutely no idea on what to do obviously.
My first thought was contouring due to the singularity but I have little experience with that.
Taylor expansion didn't occur to me until a lot later.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
Could you clarify the source and the typical integration techniques used in this book? I will have another look at it later today if I have time.I don't even know at all. When I first saw this integral I had absolutely no idea on what to do obviously.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
The slow decay of the integrand again makes things nontrivial (what contour do you suggest?), and the singularity is removable, not a pole so there is no benefit in contouring about it (for the original function, it is a pole of the complexified function, but the problem of slow decay remains).
We are in the extracurricular marathon, so post a contour integration solution if you do find one.Well the only other way I see is by contouring the first quadrant but like I said.
Too advanced.
The slow decay of the integrand again makes things nontrivial (what contour do you suggest?), and the singularity is removable, not a pole so there is no benefit in contouring about it (for the original function, it is a pole of the complexified function, but the problem of slow decay remains).
Last edited:
