HSC 2016 MX1 Marathon (archive) (1 Viewer)
- Thread starter Speed6
- Start date
- Status
- Not open for further replies.
davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon
My reason for going AD (was to go against the opposite direction of the double arrow) , was that I thought BC (like AD, going against the opposite direction of the double arrow )
My thinking is another possible solution would be:
 ?
?
What do you mean by 'order'? I am a person that likes to follow the order as well.I don't know how strict the HSC is on such things, but it is generally a bad idea to state congruences and similarities without listing the vertices in order of their correspondence (which is not the case with your statement, the angles are not in the same order).
Even in the best-case scenario that they don't mark you down for such things, I think it is still a much better idea to state things in order in the first place, so then you can directly read off the resulting statements about side lengths and angles from your similarity/congruence statement without having to refer back to the diagram to check that angles "match up".
My reason for going AD (was to go against the opposite direction of the double arrow) , was that I thought BC (like AD, going against the opposite direction of the double arrow )
My thinking is another possible solution would be:
davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon
Question:

Question:
dan964
what
Re: HSC 2016 3U Marathon
is there more information, or a diagram/context?Question:

seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: HSC 2016 3U Marathon
Congruence of polygons means you can rotate, translate, and flip one till it is "on top" of the other, and in doing so you get a pairing between vertices of the first polygon and the vertices of the second one. This pairing need not be unique, but you should state congruences and similarities so that the order of vertices are in correspondence, which is not the case in the two statements you made.
(Similarity is the same, but includes the operation of scaling).
In particular, note that if triangles ABC and XYZ are similar, then the angles A=X, B=Y, C=Z.
By order, I mean the "matching order" referred to in the question.What do you mean by 'order'? I am a person that likes to follow the order as well.
My reason for going AD (was to go against the opposite direction of the double arrow) , was that I thought BC (like AD, going against the opposite direction of the double arrow )
My thinking is another possible solution would be:
?
Congruence of polygons means you can rotate, translate, and flip one till it is "on top" of the other, and in doing so you get a pairing between vertices of the first polygon and the vertices of the second one. This pairing need not be unique, but you should state congruences and similarities so that the order of vertices are in correspondence, which is not the case in the two statements you made.
(Similarity is the same, but includes the operation of scaling).
In particular, note that if triangles ABC and XYZ are similar, then the angles A=X, B=Y, C=Z.
Last edited:
davidgoes4wce
Well-Known Member
davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon

OK you cleared it up I redid Q5 (b) and listed down the matching pair.By order, I mean the "matching order" referred to in the question.
Congruence of polygons means you can rotate, translate, and flip one till it is "on top" of the other, and in doing so you get a pairing between vertices of the first polygon and the vertices of the second one. This pairing need not be unique, but you should state congruences and similarities so that the order of vertices are in correspondence, which is not the case in the two statements you made.
(Similarity is the same, but includes the operation of scaling).

davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon
But I don't think you'd lose a mark in the HSC if you wrote the angles your way.
It probably is OK, but the book's way is probably better because it lists the vertices in matching order (like matching with the corresponding vertices in the other congruent triangle). Always writing these things in matching order will also help you keep track of which sides and angles etc. in the congruent triangle are corresponding ones, which can help as you won't need to look carefully at the diagram to see this, you can just read it off your arrangement of the vertices' letters.
But I don't think you'd lose a mark in the HSC if you wrote the angles your way.
davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon
^^^ Thanks I want to develop good habits for Circle Geometry as I'll be honest I never touched that stuff in high school and university.
^^^ Thanks I want to develop good habits for Circle Geometry as I'll be honest I never touched that stuff in high school and university.
davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon
You should probably say that opposite sides of a parallelogram/rectangle are equal.
Re: HSC 2016 3U Marathon
Are those meant to be binomial coefficients?Simplify n(n-1 1)+n(n-1 2)+...+n(n-1 n-2)
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Re: HSC 2016 3U Marathon
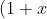^{n-1}=\binom{n-1}{0}+\binom{n-1}{1}x+\binom{n-1}{2}x^2+\dots+\binom{n-1}{n-2}x^{n-2}+\binom{n-1}{n-1}x^{n-1})



Weird question that does not have a truly neat solutionSimplify n(n-1 1)+n(n-1 2)+...+n(n-1 n-2)
Paradoxica
-insert title here-
Re: HSC 2016 3U Marathon

Last edited:
Paradoxica
-insert title here-
Re: HSC 2016 3U Marathon
integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 779
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 3U Marathon
ya and also this is 3U, which means you normally wouldn't need to use substitution if you're not asked to
Re: HSC 2016 3U Marathon
^{3/2} \right ] $from 0 to 16$ \\ =20^{3/2}-4^{3/2} = 40\sqrt{5}-8 )
ohh ye my bad thanks. Is this better?What is the derivative of x2/3
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Re: HSC 2016 3U Marathon
It's a marathon. Whilst in the HSC you're given the substitution, anything appears to be fine here.ya and also this is 3U, which means you normally wouldn't need to use substitution if you're not asked to
- Status
- Not open for further replies.