Re: Extracurricular Integration Marathon
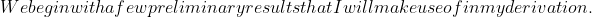
$)
$)
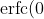 = 1, \frac{d}{dx} \text{erfc}(x) = -\frac{2}{\sqrt{\pi}} e^{-x^2})
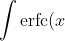 \, dx = x \text{erfc}(x) - \frac{1}{\sqrt{\pi}} e^{-x^2} + \mathcal{C}$ (established using IBP)$)
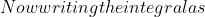
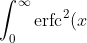 \, dx = \int_0^\infty \text{erfc}(x) \cdot \text{erfc}(x) \, dx.)
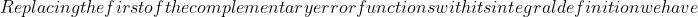
 \, dx &=\int_0^\infty \frac{2}{\sqrt{\pi}} \int^\infty_x e^{-u^2} \, du \cdot \text{erfc}(x) \, dx\\&=\frac{2}{\sqrt{\pi}} \int^\infty_0 \int^\infty_x e^{-u^2} \text{erfc}(x) \, du \,dx\\&=\frac{2}{\sqrt{\pi}}\int^\infty_0 \int^u_0 e^{-u^2} \text{erfc}(x) \, dx\,du,\end{align*})
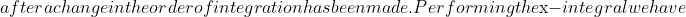
 \, dx &=\frac{2}{\sqrt{\pi}} \int^\infty_0 e^{-u^2} \left [x \text{erfc}(x) - \frac{1}{\sqrt{\pi}} e^{-x^2} \right ]^u_0 \, du\\&= \frac{2}{\sqrt{\pi}} \int^\infty_0 e^{-u^2} \left [u \text{erfc}(u) - \frac{1}{\sqrt{\pi}} e^{-u^2} + \frac{1}{\sqrt{\pi}} \right ] \, du\\&=\frac{2}{\sqrt{\pi}}\int^\infty_0 ue^{-u^2} \cdot \text{erfc}(u) \, du - \frac{2}{\pi} \int^\infty_0 e^{-2u^2} \, du + \frac{2}{\pi} \int^\infty_0 e^{-u^2} \, du\end{align*})
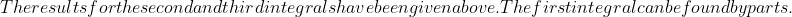
 \, du &= -\frac{1}{2} e^{-u^2} \text{erfc}(u) \Big{|}^\infty_0 - \int^\infty_0 -\frac{1}{2} e^{-u^2} \cdot -\frac{2}{\sqrt{\pi}} e^{-u^2} \, du\\ &= \frac{1}{2} - \frac{1}{\sqrt{\pi}} \int^\infty_0 e^{-2u^2} \, du\\&= \frac{1}{2} - \frac{1}{\sqrt{\pi}} \cdot \frac{\sqrt{\pi}}{2\sqrt{2}}\\&=\frac{1}{2} - \frac{1}{2\sqrt{2}}.\end{align*})
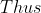
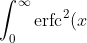 \, dx = \frac{2}{\sqrt{\pi}} \left (\frac{1}{2} - \frac{1}{2\sqrt{2}} \right ) - \frac{2}{\pi} \cdot \frac{\sqrt{\pi}}{2 \sqrt{2}} + \frac{2}{\pi} \cdot \frac{\sqrt{\pi}}{2} = \frac{2 - \sqrt{2}}{\sqrt{\pi}}.)
Nice excercise for manipulating special functions.
^2 \text{d}x \\\\ $Where erfc$(x)$ is the complementary error function.$ \\\\ $erfc$(x) = \frac{2}{\sqrt{\pi}}\int_{x}^\infty e^{-t^2} \text{d}t)
Nice excercise for manipulating special functions.
^2 \text{d}x \\\\ $Where erfc$(x)$ is the complementary error function.$ \\\\ $erfc$(x) = \frac{2}{\sqrt{\pi}}\int_{x}^\infty e^{-t^2} \text{d}t)
Here's an easier one. Fun Exercise
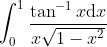
A fairly easy exercise.
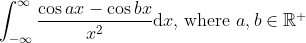
That's nice but it's not exactly an answer, since you haven't proven that the sum is the inverse hyperbolic sine of 1.
He used the Maclaurin series for the inverse hyperbolic sine (and the fact it holds at t = 1, which we can show for example by using Abel's theorem. We can show the series converges with the help of Stirling's approximation, for example).That's nice but it's not exactly an answer, since you haven't proven that the sum is the inverse hyperbolic sine of 1.
The logarithmic component can be reverted into an integral as follows:
Prove the following result:
\tan^{-1}{(x^2)}}{x^4 + 4x^2 +1}$d$x= \frac{\pi^2}{12\sqrt{2}})
There's only contour integration which is what I didn't want XD. Thanks for this completely elementary solution which I have been desiring for a long time.
You could combine that with the symmetry of the integral to cut through some of that I suppose....One way (probably pretty inefficient so am not going to bother texing it) is to just differentiate with respect to the parameters.
I let x=a^2, y=b^2, and evaluatedusing the easy result that
for a > 1.
(And chuck some absolute values around a and b if you want to allow them to be negative obviously.)
Add the two equations
Now that this is somewhere slightly more appropriate...
