-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
4 types of relations (1 Viewer)
- Thread starter Jigmey
- Start date
so y = |x-3| would become y = x+3?That's called the absolute value function, and it's defined by
Basically, you only want the magnitude of the number, not its sign.
For example,
If, then either
or
.
A useful identity to know is

Unfortunately it's not that simple. You can't "break up" the absolute value function like that.so y = |x-3| would become y = x+3?
If
You can try graphing these to visualise the effect of the absolute value function.
So, expanding on the idea:That's called the absolute value function, and it's defined by

FYI, the absolute value function is a special case of what is called the modulus (only appears in Extension 2) but which is also the basis for the use of the same vertical line symbols in vectors.
Similar questions (so you can do the originals yourself):
1(a). Explain, with an example using a y-value, why each function is many-to-one.
(i)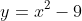
(ii)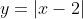
(iii)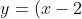x(x + 2))
(iv)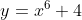
(b) Hence classify each relation below.
(i)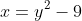
(ii)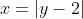
(iii)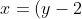y(y + 2))
(iv)
1(a) If a graph passes the vertical line test - that is, that all values of x in the domain produce a single value of y, though the y-values can be different for each x-value - and thus the graph represents a function. That function is "many-to-one" if the graph fails the horizontal line test, and thus that there exists at least one value of y that leads to multiple (more than one) values of x. If the graph passes the horizontal line test then the function is "one-to-one." All four questions in 1(a) are functions as, in each case, choosing any value of x produces only one value of y.
(i) Consider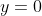 :
:
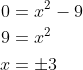
For this function, the value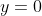 leads to two possible values of
leads to two possible values of 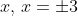 , and thus means the function is many-to-one instead of one-to-one.
, and thus means the function is many-to-one instead of one-to-one.
(ii) Consider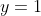 :
:
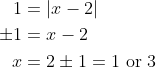
For this function, the value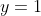 leads to two possible values of
leads to two possible values of 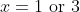 , and thus means the function is many-to-one instead of one-to-one.
, and thus means the function is many-to-one instead of one-to-one.
(iii) Consider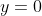 :
:
x(x + 2) \\ 0 = x - 2 \quad \text{or} \quad 0 &= x \quad \text{or} \quad 0 = x + 2 \\ x &= 0 \text{ or } \pm 2 \end{align*})
For this function, the value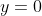 leads to three possible values of
leads to three possible values of 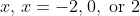 , and thus means the function is many-to-one instead of one-to-one.
, and thus means the function is many-to-one instead of one-to-one.
(iv) Consider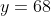 :
:
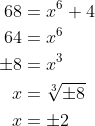
For this function, the value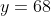 leads to two possible values of
leads to two possible values of 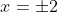 , and thus means the function is many-to-one instead of one-to-one.
, and thus means the function is many-to-one instead of one-to-one.
(b) Swapping x and y produces a relation that swaps the vertical and horizontal line results, so all of the relations in (b) will be one-to-many.
2(a). By solving for x, show that each function is one-to-one. (this method works only if x can be made the subject. Then, the relation is one-to-one if there is never more than one answer, and many-to-one otherwise.)
(i)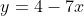
(ii)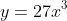
(iii)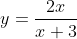
(b) Hence classify each relation below.
(i)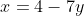
(ii)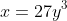
(iii)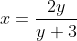
2(a)(i) and (b)(i):
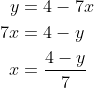
Each value of x leads to one value of y, and each value of y leads to only one value of x. In other words, the graph passes both the horizontal and vertical line tests, and we have a one-to-one function - as must the relation in (b)(i).
2(a)(ii) and (b)(ii):
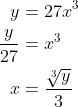
Each value of x leads to one value of y, and each value of y leads to only one value of x. In other words, the graph passes both the horizontal and vertical line tests, and we have a one-to-one function - as must the relation in (b)(ii).
2(a)(iii) and (b)(iii):
 &= 2x \\ 2xy + 3y &= 2x \\ 3y &= 2x - 2xy = 2x(1 - y) \\ \frac{3y}{2(1 - y)} &= x \end{align*})
Each value of x leads to one value of y, and each value of y leads to only one value of x. In other words, the graph passes both the horizontal and vertical line tests, and we have a one-to-one function - as must the relation in (b)(iii).
1(a). Explain, with an example using a y-value, why each function is many-to-one.
(i)
(ii)
(iii)
(iv)
(b) Hence classify each relation below.
(i)
(ii)
(iii)
(iv)
1(a) If a graph passes the vertical line test - that is, that all values of x in the domain produce a single value of y, though the y-values can be different for each x-value - and thus the graph represents a function. That function is "many-to-one" if the graph fails the horizontal line test, and thus that there exists at least one value of y that leads to multiple (more than one) values of x. If the graph passes the horizontal line test then the function is "one-to-one." All four questions in 1(a) are functions as, in each case, choosing any value of x produces only one value of y.
(i) Consider
For this function, the value
(ii) Consider
For this function, the value
(iii) Consider
For this function, the value
(iv) Consider
For this function, the value
(b) Swapping x and y produces a relation that swaps the vertical and horizontal line results, so all of the relations in (b) will be one-to-many.
2(a). By solving for x, show that each function is one-to-one. (this method works only if x can be made the subject. Then, the relation is one-to-one if there is never more than one answer, and many-to-one otherwise.)
(i)
(ii)
(iii)
(b) Hence classify each relation below.
(i)
(ii)
(iii)
2(a)(i) and (b)(i):
Each value of x leads to one value of y, and each value of y leads to only one value of x. In other words, the graph passes both the horizontal and vertical line tests, and we have a one-to-one function - as must the relation in (b)(i).
2(a)(ii) and (b)(ii):
Each value of x leads to one value of y, and each value of y leads to only one value of x. In other words, the graph passes both the horizontal and vertical line tests, and we have a one-to-one function - as must the relation in (b)(ii).
2(a)(iii) and (b)(iii):
Each value of x leads to one value of y, and each value of y leads to only one value of x. In other words, the graph passes both the horizontal and vertical line tests, and we have a one-to-one function - as must the relation in (b)(iii).



