Consider pair of line segments:
2i + 3j + lambda(-2i + 3j)
and
6i + 2j + lambda(i - 4j)
What coordinate is the intersection of both segments?
As pointed out by ultra908, question asks for the point of intersection of 2 lines:

Rewriting these vector equations in their parametric form:

Equating x and y for the 2 lines, we get after simplifying:

Using this, we get: x = 2 -2(-3) = 8 and y = 3 + 3(-3) = -6
So the point of intersection is
(8, -6)
The line L1 passes thru the point (2,3) with gradient 3/(-2) = -3/2 with eqn:
3x + 2y = 12
and L2 passes thru the point (6,2) with gradient (-4)/1 = -4 with eqn:
4x + y = 26
The point (8 ,-6) satisfies both these equations; therefore (8, -6) lies on both lines and is therefore the point of intersection of L1 and L2. This also indirectly gives me the satisfaction that I had got the value of the parameter
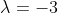
correct.
Remark
One way to specify a line is to provide one point on the line and its direction. In typical co-ord geometry this direction is the gradient.
In vector method, the direction is provided by the
direction vector (
not unique), e.g. for L1 it is
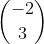
In L!: the vector eqn is based on the one point on L1,
(2,3) and the said direction vector.

