stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
This one should be easier.
dx)
This one should be easier.
dx)
Not sure if this is still active but I'll give this a go for fun (let me know if I've made any mistakes or there is an easier way). The x-ints area new one...shouldn't be too hard
Feel free to share your attempt.
Find the area bounded by x-axis and the curve
.
Not quite sure where I missed the half, but I might not have checked it properly.Your approach is correct but unfortunately a factor of 1/2 is missing somewhere.
\left(1+\pi^{x}\right)}dx=\frac{\pi}{48}-\frac{\sqrt{3}}{32}\pi+\frac{1}{8})
I believe the factor of a half comes from the identity you (incorrectly) quoted. The identity should be:Not quite sure where I missed the half, but I might not have checked it properly.
Using the identity:another one
Feel free to share your attempt.
\cos\left(x^{x}-\ln x\right)\log_{2}\left(ex\right)dx=\frac{\left(5\ln2-8\right)\sin\left(2\ln2\right)+\left(4-5\ln2\right)\sin\left(4\ln2\right)+\left(10\ln2-6\right)\cos\left(2\ln2\right)+\left(3-10\ln2\right)\cos\left(4\ln2\right)}{100\ln2})
This is the product of two functions. You cannot substitute and multiply this way.
Wow that was a long one, unfortunately didn't get it out as I'm off by a bit, can anyone see my error?
Yes well done guess it was too easy Try:
I did this a slightly different way:Since this thread is dead I thought I would post a question: Find: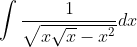
This is my first attempt but the answer‘s slightly off. On the line markedYes well done guess it was too easy Try:
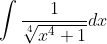
I dont think you converted from theta to x correctly. Shouldn'tThis is my first attempt but the answer‘s slightly off. On the line marked, if the denominator is
instead of
then I think the final answer is correct but I can’t find the missing negative.
Also @Qeru pls post more I was SOOOO close to gettingYes well done guess it was too easy Try:
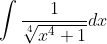
Yes, you are correct. I’m so dumb!I dont think you converted from theta to x correctly. Shouldn't, you did the reciprocal I think. Other than that you got it right.
