how do I do this question??
Sketch the graph of:
(a) arg(z + i) = arg(z − 1)
(b) arg(z + i) = arg(z − 1) + π
An easy way to think of this is to recognise that
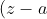)
refers to the vector from

to

.
So,
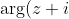=\arg(z-1))
means that the direction from
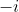
to

is the same as the direction from 1 to

.
Let
A correspond to the point where
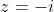
and
B correspond to the point
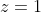
. For any point
Z (corresponding to the complex number

) not on the line through
A and
B,
ABZ would be a triangle with three non-zero angles. It follows that the directions of vectors
AZ and
BZ cannot be the same, and thus that all points in the locus must lie on the line through
A and
B... though not all points are necessarily included.
The points
A and
B themselves cannot be in the locus as, in each case, one of the required arguments is defined and the other is not because
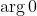
is undefined.
The points between
A and
B (where
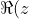\in(0,\ 1))
) are also excluded from the locus as in this region
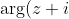=\frac{\pi}{4})
but
=-\frac{3\pi}{4})
In other words, between
A and
B
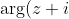-\arg(z-1)=\frac{\pi}{4}--\frac{3\pi}{4}=\pi)
and so the interval
AB (but excluding its end points) is the locus for part (ii),
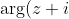=\arg(z-1)+\pi)
.
For all points on
AB with
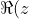\in(-\infty,\ 0)\cup(1,\ +\infty))
, the required arguments are the same because the directions of the vectors
AZ and
BZ are the same, and so those points are included in the locus of
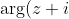=\arg(z-1))
.