A remark on Q13c)ii).
It had a nice trap where you had to recognise that f'(x) and g'(x) are undefined at the points (1,0) and (-1,0) but these are points where the f(x) and g(x) are defined.
So technically speaking you can only say that since their derivatives are
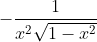
then
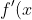=g'(x)\quad\text{ for }0<x<1\text{ and }-1<x<0)
Therefore you can only really claim that
=g(x)+c\quad\text{ for }0<x<1\text{ and }-1<x<0)
This would suggest that simply substituting in say x = 1 to find c has some rigour issues as it doesn't quite fit that domain (even though it works out).
I think the intended solution was for students to recognise that since
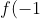 = g(-1) = 0)
 = g(1) = 0)
then f(x) and g(x) share common points at x = -1 and x = 1.
From part (i), they have the same gradient behaviour in the domain -1 < x < 0 but have a common point at x = -1 on the "edge" of that domain. This means that
 = g(x)\quad\text{ for }-1 \leq x < 0)
Similarly, they have the same gradient behaviour in the domain 0 < x < 1 but have a common point at x = 1 on the "edge" of that domain. This means that
 = g(x)\quad\text{ for }0 < x \leq 1)
