-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Proofs help (Proof by Contradiction) (1 Viewer)
- Thread starter O01x
- Start date
1. cos(n+1) = 2cos(n)cos(1) - cos(n-1)
Need help with part b) from the first question and the other 2 questions.
Suppose cos 1 is rational.
It follows that cos 1,2,3,4,5.... is rational.
But, there exists cos n such that cos n is irrational, e.g., cos 30.
2. can't work out the question. If a is not a factor of b, it is obviously not factor of b+1 if a>= 2.
3. y^2 = x^2 -1
y^2 = (x+1)(x-1)
by definition, a square number is made up of the product of the same numbers.
if b is an integer, it must be a factor of +- itself, b or -b. If it is not a factor of any natural number, it is an integer that is not a natural number and is thus 0.Question 2 was
Prove that if b is an integer and b is not a factor of k for every k (Natural Numbers), then b=0
this question seems like nonsense tho, maybe im understanding it wrong.
Last edited:
a) is just rational root theorem. Oh you want by contradicton. AssumeMore questions (Contradiction) :
Explain why x^3+x+1=0 has no rational roots
Prove that there exists no integer a and b for which 21a+30b=1
b) Assume a and b are integers. The expression is equivalent to:
1. Prove that there is no integer that leaves a remainder of 2 on division by 6, and also leaves a remainder of 7 on division by 9.
2. Prove that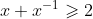 for any value
for any value 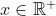
3. Prove that no integer has a square that leaves a remainder of 3 on division by 4.
4. Prove that if a right angled triangle has sides of lengths ,
,  , and
, and  (where
(where  is the length of the hypoteneuse), and another right angled triangle has sides of lengths
is the length of the hypoteneuse), and another right angled triangle has sides of lengths 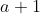 ,
,  , and
, and 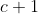 (where
(where 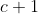 is the length of the hypoteneuse), then at least one of
is the length of the hypoteneuse), then at least one of  ,
,  , and
, and  is not an integer.
is not an integer.
5. Prove that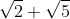 is irrational.
is irrational.
6(a). Suppose that and
and  are positive integers. Find real constants
are positive integers. Find real constants 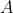 and
and 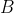 such that
such that
(a+b+1)} = \frac{A}{a+b} + \frac{B}{a+b+1})
(b). Hence, or otherwise, show that, if is a positive integer, then
is a positive integer, then
(n+k+1)}}<\frac{1}{n+1})
(c). You may use, without proof, the fact that
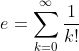
in order to prove that is irrational.
is irrational.
2. Prove that
3. Prove that no integer has a square that leaves a remainder of 3 on division by 4.
4. Prove that if a right angled triangle has sides of lengths
5. Prove that
6(a). Suppose that
(b). Hence, or otherwise, show that, if
in order to prove that
Last edited:
Qeru, just a quick reminder that you needa) is just rational root theorem. Oh you want by contradicton. Assume(where a and b are non zero integers) is a root. Then:
. The parity of the LHS is different to the parity of the RHS so contradiction.
As it happens, this is necessary for the parity argument that you are making in this case. You are stating that the LHS is odd and the RHS is even, which is true but only because at least one of
Further, examiners will not necessarily know what you mean by LHS and RHS have different parity. It would be simpler in this case to note
How does this follow? You could have some combination of a and b which equals zero (since either a or b could be negative).Further, examiners will not necessarily know what you mean by LHS and RHS have different parity. It would be simpler in this case to noteand so
, producing the necessary contradiction.
True... an alternative is then thatHow does this follow? You could have some combination of a and b which equals zero (since either a or b could be negative).
How could we do Question 4)1. Prove that there is no integer that leaves a remainder of 2 on division by 6, and also leaves a remainder of 7 on division by 9.
2. Prove thatfor any value
3. Prove that no integer has a square that leaves a remainder of 3 on division by 4.
4. Prove that if a right angled triangle has sides of lengths,
, and
(where
is the length of the hypoteneuse), and another right angled triangle has sides of lengths
,
, and
(where
is the length of the hypoteneuse), then at least one of
,
, and
is not an integer.
5. Prove thatis irrational.
6(a). Suppose thatand
are positive integers. Find real constants
and
such that
(b). Hence, or otherwise, show that, ifis a positive integer, then
(c). You may use, without proof, the fact that
in order to prove thatis irrational.
Assume a,b and c are integers. We know from pythagoras:How could we do Question 4)
But addition is closed for the integers so the LHS must be an integer but the RHS is clearly not so contradiction. So atleast one of a,b or c is not an integer.

