is an acid-base reaction now defined irrespective of products and only based on reagents?
How an acid-base reaction is defined really depends on what model is used for the definition. If I look online, I will find that the
pKa for methane is about 50. If I do the calculation as you have learned it, I can calculate that a 0.0100 mol L
-1 of methane has a
pH of 26. This result is meaningless in the theory that you have covered which points to the model used to find the result is flawed in this situation... but it doesn't invalidate the calculation that a 0.100 mol L
-1 solution of acetic acid (
pKa = 4.76) has a
pH of 2.88 at 298 K.
In some ways, the topic of acids and bases is an excellent example of an important aspect of models, extending way beyond chemistry.
In both science and mathematics, much early learning concerns learning about methods of problem solving and situations with a single answer that represents (in some sense) "truth". Mathematics helps us to learn that an answer can be found in multiple ways and thus that there are significant differences between methods and outcome.
Take a simple example like the equation
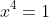
.
I can square root to get
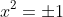
, reject the possibility of
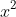
being negative, square root again, and reach a solution
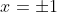
. If I am dealing solely in cardinals, I have the single answer
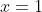
.
OR, I can factorise
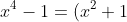(x^2-1) = (x^2+1)(x+1)(x-1))
, recognise that this must be zero from the starting equation, and thus have solutions where
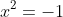
,
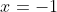
, and
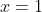
. I get the same result on rejecting
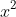
being negative.
OR, from the factorisation, I can form two quadratic equations,
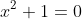
and
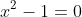
, each of which I can solve using the quadratic equation:
(1)}}{2(1)} = \frac{0 \pm \sqrt{-4}}{2} = \frac{\pm 2\sqrt{-1}}{2} = \pm \sqrt{-1})
and
(1)}}{2(1)} = \frac{0 \pm \sqrt{4}}{2} = \frac{\pm 2}{2} = \pm 1)
I can see my four solutions are
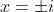
and
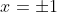
over
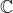
or, over
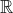
, the two solutions are
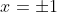
, as was found above.
Of course, the earlier approaches will also find the
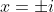
solutions if the rejection of an
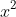
is negative case is recognised as reasonable over
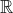
but not over
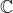
.
Which of these is "correct" or "true" depends on whether the outcome is considered over
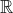
or over
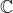
, but the answers are the same. Which of the methods is preferable has no universal answer as they differ in efficiency but not in accuracy.
In other words, one thing Maths is helping students to learn is that there are different ways to approach a problem which might be more or less simple / efficient but which still lead to the same outcome. This insight is just as important for any field of problem solving, and even one where there is no clear cut standard of accuracy / "truth" by which to determine an outcome. An essay on the exploration of a theme in an English set text can be thought of as a problem allowing different methods and different outcomes that can be assessed for the quality of the argument, persuasiveness of the evidence, and significance of the outcome in response to the problem.
Acids and bases allows students to explore some of these ideas in a scientific context. In learning about historical conceptions, Arrhenius theory, Lowry-Bronsted theory, and even Lewis theory, what is developed is NOT a progression from less accurate to more accurate theories. It is an exploration of theories that are more or less suitable to understanding and interpreting evidence through different contextual lenses. Some students may think that Lowry-Bronsted theory is "better" or more accurate / true than Arrhenius theory, but more able students will hopefully realise that each is useful for different contexts and so can be used selectively depending on contexts. There are plenty of contexts in which each is applicable and will yield comparable outcomes making each useful for that context without making either superior than the other. That a theory is inapplicable to situation A does not make its validity / utility to situation B any different, it just makes the theory not useful for A.
This idea arises all over the place. If I want to determine how high a projectile thrown at 10 m s
-1 on Earth will rise, simple two dimensional motion will give a reasonable answer. The same problem with an initial speed of 10 km s
-1 will need a model that includes other factors. If I want to launch a rocket to Mars, yet more factors are needed. Does this make the rocket model better for the simple thrown rock example? No - because the difference is in the applicability of the models and the reasonableness of their underlying assumptions. I am not going to model a car travelling at 60 km h
-1 by rejecting Newtonian notions in favour of quantum mechanics because the differences in such a case will be trivial, no matter that quantum mechanics is arguable more "true" as it considers more factors. Similarly, I need not solve a problem where Arrhenius theory is perfectly applicable by using Lewis theory even if Lewis theory is a more broadly applicable theoretical framework.
Models are used as tools in a myriad of human contexts. Much early learning presents this as accessing "truth" without really studying limitations, usefulness, and the idea of what truth actually might be. The acids and bases topic can be treated as requiring guessing about which model is sought in a given circumstance, but is much more significantly trying to help students to recognise that models are not about truth nor about which is "correct" in a given circumstance. By nature, models are about usefulness, applicability and limitations, and judgement about when they can be used or whether what they produce is reasonable.

