di)
(x+4) > 2 / (x+3)
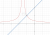
The graph will look like this
View attachment 30646
So if you can find the intersection points you can determine the values that satisfy the inequality
(x+4) = 2 / (x+3) (Note x cannot equal -3)
=> (x+3)(x+4) = 2
=> x^2 +7x +12 - 2 =0
=> x^2 +7x +10 =0
=> (x+5)(x+2) = 0
=> x= -5, -2
From this we can determine y = -1, 2 respectively.
The inequality is satisfied when " -5 < x < -3 or x>-2"
ii)
Based on the graph we can determine the inequality is satisfied when x<-5 or (x>-2 and x !=3
Alternative for d i)
(x+4)(x+3)^2 > 2(x+3) (We need to multiply by (x+3)^2 as x+3 could be negative and result in change of the sign of the inequality)
=> (x+4)(x+3)^2 -2(x+3) > 0
=> (x+3) * [ (x+4)(x+3) -2 ] >0
=> (x+3) * [x^2 +7x + 10] > 0
=> (x+3) * (x+5) * (x+2) > 0
Sketching this we can get the answer.
Alt for dii)
(x+4)|x+3| -2 >0
Then consider the case when x < -3
=> (x+4)(-x-3) -2 >0
or the case when x>= -3
(x+4)(x+3) -2 >0