Let gradient be

First we will sub the point (1,-2) and

into point gradient formula
=m(x-1)\\y=mx-(m+2))
Since the line and the parabola touch each other, we have to solve them simultaneously
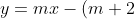\longrightarrow \textcircled{1}\\y=x^2\longrightarrow \textcircled{2})
Sub
into
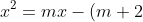\\x^2-mx+(m+2)=0)
Using quadratic formula we can solve for x and

}}{2}\\x=\frac{m\pm\sqrt{m^2-4m-8}}{2})
However since the original line is tangent to the curve, there would only be one value for x, hence
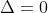
which means that
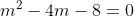
}}{2}\\\\m=\frac{4\pm\sqrt{48}}{2}\\\\m=2\pm2\sqrt{3})
Therefore the two equations for the line are...
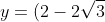(x-1)-2\ \text{and}\ y=(2+2\sqrt{3})(x-1)-2)