Question help!!!! ASAP (1 Viewer)

Run hard@thehsc · Jun 8, 2022

How would you find the amplitude in such cases?

Epicman69 · Jun 8, 2022

Auxilliary angles?

Run hard@thehsc · Jun 8, 2022

Epicman69 said:
Auxilliary angles?

fair - so we can't really use the acceleration equation then....

Epicman69 · Jun 8, 2022

Run hard@thehsc said:
fair - so we can't really use the acceleration equation then....

Yea I don't think so, what is -w^2(x-c) gonna give us for amplitude. Although I haven't finished the SHM topic yet, so better to check with ur teacher, maybe there is a better way.

5uckerberg · Jun 9, 2022

Run hard@thehsc said:
View attachment 35762
View attachment 35763
How would you find the amplitude in such cases?

Okay, @Run hard@thehsc chill. In this question look at the order in which we have to find the various properties.

First, prove the motion is SHM.
Second, find the centre of motion.
Third, find the period.
Lastly, find the amplitude.

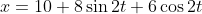
To begin with, this one where $x=10+8\sin{2t}+6\cos{2t}$ we need to start by moving 10 to the other side so that we are just left with a trigonometric function which will serve us well.

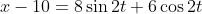
$x-10=8\sin{2t}+6\cos{2t}$ . Apply, auxiliary angles here.
$R\cos{\alpha}=8$
$R\sin{\alpha}=6$
$R^{2}=100, R=10$
$\tan{\alpha}=\frac{3}{4}$
$\alpha=\tan^{-1}\left(\frac{3}{4}\right)$

Once you have this in the basket then we use complementry angles to say that $x-10=10\sin\left(2t+\tan^{-1}\left(\frac{3}{4}\right)\right)$ . using the fact that with auxiliary angles we want something of the form $R\sin{2t}\cos{\alpha}+R\cos{2t}\sin{\alpha}=R\sin\left(2t+\alpha\right)$ which is $10\sin\left(2t+\tan^{-1}\left(\frac{3}{4}\right)\right)$ if we sub everything in.

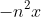
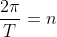
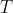
Differentiate twice to get acceleration because for SHM the acceleration is in the form of $-n^{2}x$ or $-n^{2}\left(x-c\right)$ where c is the centre of motion and n is what we use to find period through $\frac{2\pi}{T}=n$ where n is the number of cycles and $T$ is the time it takes to complete the cycle.

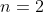
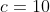
Upon performing differentiation twice this is what we will have $\ddot{x}=\frac{d^{2}x}{dt^{2}}=-40\sin\left(2t+\tan^{-1}\left(\frac{3}{4}\right)\right)$ . Hang, on is this simply $-4\left(10\sin\left(2t+\tan^{-1}\left(\frac{3}{4}\right)\right)\right)$ and then this is just simply $-4\left(x-10\right)$ where it is in the form $-n^{2}\left(x-c\right)$ where $n=2$ & $c=10$ . This proves that the motion is simple harmonic.

The centre of motion as we have discussed is 10.

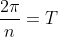
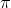
The period is $\frac{2\pi}{n}=T$ which is $\pi$ because $\frac{2\pi}{2}=\pi$ .

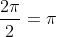
Now, @Epicman69 the moment of truth has arrived.

To find the amplitude we go back all the way to the start of the question after the auxiliary angles were done and the centre of motion is on the RHS with the auxiliary angle. $x=10+10\sin\left(2t+\tan^{-1}\left(\frac{3}{4}\right)\right)$ . Now we see that the particle oscillates between 0 and 20 because of the sine function so therefore, our amplitude will be half of that which will give us 10.

b) Should be straight forward let x=0 and then the rest is calculations.

Question help!!!! ASAP (1 Viewer)

Run hard@thehsc

Well-Known Member

Epicman69

Active Member

Run hard@thehsc

Well-Known Member

Epicman69

Active Member

5uckerberg

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)