I don't really get what you're trying to say, I pointed out that the original integral is
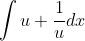
so it doesn't make any sense in the first place that dividing by u on the top and bottom of the fraction would lead to a mistake since
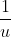
is already present (if it was 0 it's not like they can cancel), it's not being newly introduced or anything.
For more general cases: (technique being multiplying top and bottom by something)
When evaluating indefinite integrals the technique is fine, indefinite integrals are more lenient because it simply means taking the derivative of the indefinite integral gives you the integrand. That's why
blob063540 's answer would pretty much always be considered correct and you can pretty much always multiply the top and bottom by something without considering anything else.
For definite integrals you need to consider the discontinuity since it can change the answer (same with the sign for blob's answer). So I believe for regular types of functions the discontinuity can either be a pointwise discontinuity or a jump discontinuity. If you do it with partial fractions (you can't always) and get something with no discontinuity then it doesn't matter, this is a better antiderivative. If you integrate over the limits a, c
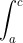
where the discontinuity is b, a<b<c, then the definite integral becomes
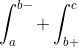
idk if that's the right notation. That's mostly for jump discontinuity because the pointwise discontinuity doesn't matter unless the interval is at the discontinuity then you have to take limits for its lower/upper bound.




