-
Looking for HSC notes and resources? Check out our Notes & Resources page
normal force in banked versus inclined planes (1 Viewer)
- Thread starter anonymoushehe
- Start date
liamkk112
Well-Known Member
- Joined
- Mar 26, 2022
- Messages
- 1,078
- Gender
- Female
- HSC
- 2023
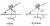
here \neq mg ) though. you also have the
though. you also have the  ) term which you need to account for. that's when there's friction present which keeps the car at a constant radius up the bank, which makes things a whole lot messier (and also isn't in the syllabus so dw about it)
term which you need to account for. that's when there's friction present which keeps the car at a constant radius up the bank, which makes things a whole lot messier (and also isn't in the syllabus so dw about it)
if there's no friction present, then ignore the whole green part. now, taking it back to the inclined plane situation, there was no centripetal force needed. this told us that we could break up the "mg" force into two components (one parallel to the plane, one perpendicular) and this told us that)
now here, can we do the same? the answer is yes, but it would be a bit redundant because now the centripetal force is involved. remember that the centripetal force is going to point horizontally, and we care about this force. so if we resolve the mg into one parallel to the plane and one perpendicular, this tells us nothing about what the centripetal force is doing. this is why in the inclined plane, we resolved mg, but now we're resolving the normal force. if we do newton's law we then get
, F_N\cos(\theta)=mg )
which is a solution that gives us info about the centripetal force. now it also kind of makes sense why we get different normal forces; in one we are getting a pull horizontally as well as downwards (giving us a strong normal force), and in the other we are only really getting a pull from the gravitational force.
if there's no friction present, then ignore the whole green part. now, taking it back to the inclined plane situation, there was no centripetal force needed. this told us that we could break up the "mg" force into two components (one parallel to the plane, one perpendicular) and this told us that
now here, can we do the same? the answer is yes, but it would be a bit redundant because now the centripetal force is involved. remember that the centripetal force is going to point horizontally, and we care about this force. so if we resolve the mg into one parallel to the plane and one perpendicular, this tells us nothing about what the centripetal force is doing. this is why in the inclined plane, we resolved mg, but now we're resolving the normal force. if we do newton's law we then get
which is a solution that gives us info about the centripetal force. now it also kind of makes sense why we get different normal forces; in one we are getting a pull horizontally as well as downwards (giving us a strong normal force), and in the other we are only really getting a pull from the gravitational force.
wizzkids
Well-Known Member
- Joined
- Jul 13, 2016
- Messages
- 347
- Gender
- Undisclosed
- HSC
- 1998
@anonymoushehe
Yes there are two cases for the normal force.
The problem here is you haven't told us what is the motion of the object on the inclined plane. I agree with liamkk112 that you should discard those green vectors, they are distracting you from a proper understanding the free-body diagram and the motion of the object.
Case 1. When the object is static on a straight inclined plane, the normal force is just FN=mg.cosθ
If there was zero friction, the object would slide down the inclined plane under the influence of the resultant vector R as shown below.

Case 2. When the object is dynamic on a banked curved inclined plane, e.g. a car executing uniform circular motion around a banked track, then the normal force is greater. This is a real effect. Watch a NASCAR race. As the race cars enter a banked curve at high speed, the car body gets closer to the track, the suspension gets lower because there is more normal force on the suspension springs. The car sits lower on the track. Why? Because the force vectors on the car have increased. The driver inside the car also feels these increased downward forces as he enters the curve. As a Physics student, I hope you can identify that it is in fact the driver's inertia that creates the impression on the driver of more downwards force, because he is now in an accelerating frame of reference.
The horizontal component of the normal force now provides a centripetal force R towards the centre of curvature of the track. If the speed of the car is optimum, the motion of the car does not slide down the inclined plane, it stays put on the inclined plane and the car executes UCM.
If the car enters into the curve too fast the resultant vector R is insufficient to accelerate the car towards the centre, and the car spirals up the banking thus increasing the radius of curvature of its path.
If the car enters the curve too slow the resultant vector is more than is required and the car spirals down the banking, thus decreasing the radius of curvature of its path.
So in summary, yes there are two cases for the normal force vector. Does that make sense?
Yes there are two cases for the normal force.
The problem here is you haven't told us what is the motion of the object on the inclined plane. I agree with liamkk112 that you should discard those green vectors, they are distracting you from a proper understanding the free-body diagram and the motion of the object.
Case 1. When the object is static on a straight inclined plane, the normal force is just FN=mg.cosθ
If there was zero friction, the object would slide down the inclined plane under the influence of the resultant vector R as shown below.

Case 2. When the object is dynamic on a banked curved inclined plane, e.g. a car executing uniform circular motion around a banked track, then the normal force is greater. This is a real effect. Watch a NASCAR race. As the race cars enter a banked curve at high speed, the car body gets closer to the track, the suspension gets lower because there is more normal force on the suspension springs. The car sits lower on the track. Why? Because the force vectors on the car have increased. The driver inside the car also feels these increased downward forces as he enters the curve. As a Physics student, I hope you can identify that it is in fact the driver's inertia that creates the impression on the driver of more downwards force, because he is now in an accelerating frame of reference.
The horizontal component of the normal force now provides a centripetal force R towards the centre of curvature of the track. If the speed of the car is optimum, the motion of the car does not slide down the inclined plane, it stays put on the inclined plane and the car executes UCM.
If the car enters into the curve too fast the resultant vector R is insufficient to accelerate the car towards the centre, and the car spirals up the banking thus increasing the radius of curvature of its path.
If the car enters the curve too slow the resultant vector is more than is required and the car spirals down the banking, thus decreasing the radius of curvature of its path.
So in summary, yes there are two cases for the normal force vector. Does that make sense?
Attachments
-
59.6 KB Views: 21
Last edited:
justletmespeak123
Active Member
- Joined
- Oct 14, 2024
- Messages
- 265
- Gender
- Male
- HSC
- 2024
tldr. can u please prove why the net force is directly down along the slope for static but horizontal in dynamic (circular motion) this confused me too... please use any math at your dispoal@anonymoushehe
Yes there are two cases for the normal force.
The problem here is you haven't told us what is the motion of the object on the inclined plane. I agree with liamkk112 that you should discard those green vectors, they are distracting you from a proper understanding the free-body diagram and the motion of the object.
Case 1. When the object is static on the inclined plane, the normal force is just FN=mg.cosθ
If there was zero friction, the object would slide down the inclined plane under the influence of the resultant vector R as shown below.
View attachment 46074
Case 2. When the object is dynamic on the inclined plane, e.g. a car executing uniform circular motion around a banked track, then the normal force is greater. This is a real effect. Watch a NASCAR race. As the race cars enter a banked curve at high speed, the car body gets closer to the track, the suspension gets lower because there is more normal force on the suspension springs. The car sits lower on the track. Why? Because the force vectors on the car have increased. The driver inside the car also feels these increased downward forces as he enters the curve. As a Physics student, I hope you can identify that it is in fact the driver's inertia that creates the impression on the driver of more downwards force, because he is now in an accelerating frame of reference.
The horizontal component of the normal force now provides a centripetal force R towards the centre of curvature of the track. If the speed of the car is optimum, the motion of the car does not slide down the inclined plane, it stays put on the inclined plane and the car executes UCM.
If the car enters into the curve too fast the resultant vector R is insufficient to accelerate the car towards the centre, and the car drifts up the banking thus increasing the radius of curvature of its path.
If the car enters the curve too slow the resultant vector is more than is required and the car drifts down the banking, thus decreasing the radius of curvature of its path.
So in summary, yes there are two cases for the normal force vector. Does that make sense?
Aeonium
zero sugar, zero ice
- Joined
- May 19, 2022
- Messages
- 638
- Gender
- Undisclosed
- HSC
- N/A
u lazy fuck just read ittldr
wizzkids
Well-Known Member
- Joined
- Jul 13, 2016
- Messages
- 347
- Gender
- Undisclosed
- HSC
- 1998
In my post above I described the displacement of a car in two different experiments. Here is a more mathematical reasoning.
In the static experiment, the car slides down the inclined plane. That is the car's displacement with respect to time.
Velocity is the first derivative of displacement with respect to time, so velocity points down the inclined plane.
Acceleration is the second derivative of displacement with respect to time, so acceleration also points down the inclined plane. The net force vector is parallel to the acceleration vector, i.e. it must point down the inclined plane.
OK, in the dynamic experiment, displacement is described by a horizontal circle, because the car is executing uniform circular motion (UCM).
Following similar reasoning to the static case, the velocity is the first derivative of displacement, it is a tangent to the circle.
Acceleration is the second derivative of displacement, it is a vector pointing towards the centre of curvature of the track. The net force vector is parallel to the acceleration vector, i.e. it must point towards the centre of curvature of the track.
In the static experiment, the car slides down the inclined plane. That is the car's displacement with respect to time.
Velocity is the first derivative of displacement with respect to time, so velocity points down the inclined plane.
Acceleration is the second derivative of displacement with respect to time, so acceleration also points down the inclined plane. The net force vector is parallel to the acceleration vector, i.e. it must point down the inclined plane.
OK, in the dynamic experiment, displacement is described by a horizontal circle, because the car is executing uniform circular motion (UCM).
Following similar reasoning to the static case, the velocity is the first derivative of displacement, it is a tangent to the circle.
Acceleration is the second derivative of displacement, it is a vector pointing towards the centre of curvature of the track. The net force vector is parallel to the acceleration vector, i.e. it must point towards the centre of curvature of the track.
Last edited: