Yes, you can.
For part (ii), take
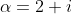
and
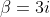
.
We are given that
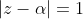
and can calculate that
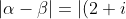 - 3i| = |2 - 2i| = \sqrt{2^2 + (-2)^2} = 2\sqrt{2})
.
We seek
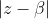
.
Applying the triangle inequality gives us that:
 + (\alpha - \beta)| \\ 1 + 2\sqrt{2} &\ge |z - \beta| \\ |z - \beta| &\le 1 + 2\sqrt{2} \end{align*})
And similarly, that:
 + (\alpha - z)| \\ |z - \beta| + 1 &\ge |\alpha - \beta| \qquad \text{as $|\alpha - z| = |-1(z - \alpha)| = |-1||z - \alpha| = 1 \times 1 = 1$} \\ |z - \beta| &\ge 2\sqrt{2} - 1 \end{align*})
Combining these:
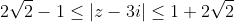
Note, also, that the method generalises, to:
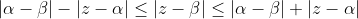
is the result without any substitutions.
Applying it to part (i), we use:
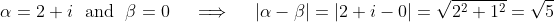
and so, by substitution, we can confirm
@Drongoski's answer, that
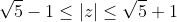
We can also expand the method to a circle with any centre

and any other point on the Argand Diagram,
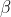
. This can provide a quick check for analogous MX1 vector problems.
It can even be applied to cases like
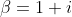
, which actually lies on the locus
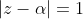
, as:
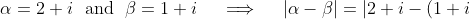| = |1| = 1)
and so yields the (expected) result, that the distance must be between zero and the length of the diameter:
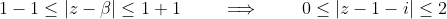
and
.
and can calculate that
.
.
