-
Looking for HSC notes and resources? Check out our Notes & Resources page
Arg qs. (1 Viewer)
- Thread starter =)(=
- Start date
ExtremelyBoredUser
Bored Uni Student
The normal way for Q.22 is to simply do a vector diagram and it might even be better;
 however
however  > arg(w_1) ) so when you draw these vectors, you would get w_1 vector having a larger argument than w_2 but the same distance. You should realise that you can create a parallelogram.
so when you draw these vectors, you would get w_1 vector having a larger argument than w_2 but the same distance. You should realise that you can create a parallelogram.
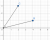
Sample of a graph you should draw (not to scale)

Through parallelogram law.
AB + AC = AD
and AD bisects both AB and AC so therefore
 = \frac{1}{2} (arg(w_1) + arg(w_2)))
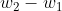 is simply CD and you can do this through vector addition.
is simply CD and you can do this through vector addition.
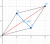
As you can see, the vector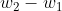 is perpendicular to the vector
is perpendicular to the vector 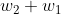 and hence there is a right angle subtended.
and hence there is a right angle subtended.
Therefore
 = arg(w_2 + w_1) - \frac{\pi}{2} )
 = \frac{\alpha_1 + \alpha_ 2 - \pi}{2} )
As required. This is the proper way I presume you are supposed to answer the question as this is under the vectors chapter and it is simply just geometric reasoning however I also used another way which might not be as proper/conventional but nonetheless is another way.
Method 2:
 as both modulus are equal to 1
as both modulus are equal to 1
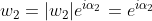
By definition of complex numbers. You can write them in mod-arg form if that is more clearer.

)
 ) Let theta just be the argument of
Let theta just be the argument of 
 ) converting - i into eulers form (you can do this in mod arg remember)
converting - i into eulers form (you can do this in mod arg remember)
 )
As you can see now, it is in the complex number form as I showed above.
hence
 = \frac{\alpha_1 + \alpha_2 -\pi}{2} )

Sample of a graph you should draw (not to scale)

Through parallelogram law.
AB + AC = AD
and AD bisects both AB and AC so therefore

As you can see, the vector
Therefore
As required. This is the proper way I presume you are supposed to answer the question as this is under the vectors chapter and it is simply just geometric reasoning however I also used another way which might not be as proper/conventional but nonetheless is another way.
Method 2:
By definition of complex numbers. You can write them in mod-arg form if that is more clearer.
As you can see now, it is in the complex number form as I showed above.
hence
Last edited:
YourLocalDumbAss
Well-Known Member
eddie woo, take that mask off NOW!The normal way for Q.22 is to simply do a vector diagram and it might even be better;
however
so when you draw these vectors, you would get w_1 vector having a larger argument than w_2 but the same distance. You should realise that you can create a parallelogram.
View attachment 33418
Sample of a graph you should draw (not to scale)
View attachment 33419
Through parallelogram law.
AB + AC = AD
and AD bisects both AB and AC so therefore
is simply CD and you can do this through vector addition.
View attachment 33420
As you can see, the vectoris perpendicular to the vector
and hence there is a right angle subtended.
Therefore
As required. This is the proper way I presume you are supposed to answer the question as this is under the vectors chapter and it is simply just geometric reasoning however I also used another way which might not be as proper/conventional but nonetheless is another way.
Method 2:
as both modulus are equal to 1
By definition of complex numbers. You can write them in mod-arg form if that is more clearer.
Let theta just be the argument of
converting - i into eulers form (you can do this in mod arg remember)
As you can see now, it is in the complex number form as I showed above.
hence
 = \frac{\alpha_1 + \alpha_2 -\pi}{2} )
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
For Q22 the work is cut out for you.
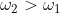 and that using vector addition you will see what I was going to bring up. Ah yes, I also was going to bring up the average of the two arguments as well but Extremely Bored User bought it up using the parallelogram law so thanks for that. Anyways this was my approach to this question.
and that using vector addition you will see what I was going to bring up. Ah yes, I also was going to bring up the average of the two arguments as well but Extremely Bored User bought it up using the parallelogram law so thanks for that. Anyways this was my approach to this question.
For Q22 this will be my explanation. From the diagram given one can say that
Attachments
-
83.8 KB Views: 19
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
Conjugate root theorem which is  where
where 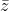 has a negative version of the imaginary part of the complex number.
has a negative version of the imaginary part of the complex number.
For future students of Mathematics, Extension II please note that suppose we have an imaginary number calling it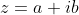 and that
and that  what is happening is that we are using the fact that
what is happening is that we are using the fact that |^{2}=(a+ib)(a-ib)=a^{2}+b^{2}-aib+aib=a^{2}+b^{2}) .
.
Please play around with this idea until it becomes second nature
For future students of Mathematics, Extension II please note that suppose we have an imaginary number calling it
Please play around with this idea until it becomes second nature
Last edited:
ExtremelyBoredUser
Bored Uni Student
View attachment 33429
How would you do this. I get argz-argz+4 =3pi/4 meaning the angle between the two points is 3pi/4 but i don't understand how a section of a circle is produced from that
General rule is that you start from the LHS, so arg(z) and you move anticlockwise till you reach the other point in RHS so arg(z+4).
This means you would start at point 0 from arg(z) and move anticlockwise to point -4 as from arg(z+4).
This is the desired locus but you can't really tell it from first glance.

So to recognise its a section;
note that the angle at the centre is double of the angle at the circumference. I forgot what the name is but that is one property. 3pi/4 * 2 = 3pi/2 but that is over the domain for a triangle so subtracting by 2 you should get -pi/2 which means the angle will be under the axis.
Now angle AFB doesn't really help much but angle EAB will. Recognise that the centre must have an angle of 90 degrees when connecting from A and B.
You would first draw the line from A or B to a centre point (which you wouldnt know)

You wouldn't know exactly the points as you wouldn't use a graphing software but the diagram should be something like this. 90 degrees on angle AEB. Now you can deduce that the angles for triangle ADE is 90,45,45 through the diagram and vice versa with EBD.
You already know the midpoint is -2 so therefore the vector AD would have a magnitude of 2. Using trig you can find the vector AE which will consequently be the radius.
Likewise you can find the point of the centre through trig.

The centre would simply be the distance of vector DE.
Pythagoras theorem would give you 2 and you can just find the coordinate of E through going 2 down from D.
So E = (-2,-2)
Now you can draw out the region through.
is the equation of the circle.
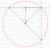
Of course only the region from point 0 to point -4 anticlockwise should be coloured in and the rest should be lined.
You wouldn't need to go to this much depth/effort but its good to understand whats going on before you do the region. For me, I can recognise when it will be a section of the circle as required as given by the equation of the arg but thats the reasoning I used to convince myself, there might be a better way to address this but its what made sense for me.
Last edited:
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,102
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
View attachment 33429
How would you do this. I get argz-argz+4 =3pi/4 meaning the angle between the two points is 3pi/4 but i don't understand how a section of a circle is produced from that
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
The first thing one would need to do is to note thatView attachment 33429
How would you do this. I get argz-argz+4 =3pi/4 meaning the angle between the two points is 3pi/4 but i don't understand how a section of a circle is produced from that
A common way to tackle this type of question is instead of using graphing software as ExtremelyBoredUser said you can observe a sunset where the sun is gradually descending below the horizon of our eyes and we can use that to find the locus around the edge of the sun. Go and watch some sunsets when the weather is nice and visually draw the locus around the sun with your finger. This is a helpful way to gain an intuition for questions that require us to sketch the locus of the argument.
View attachment 33429
How would you do this. I get argz-argz+4 =3pi/4 meaning the angle between the two points is 3pi/4 but i don't understand how a section of a circle is produced from that
While you are looking at the locus of points
involves
So, draw co-ordinates axes, label the origin as
Your locus is then the set of points
Now, if the locus had been
For
If
If
YourLocalDumbAss
Well-Known Member
@ExtremelyBoredUser’s identity has been leaked
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
Part a is quite easy to dissect. Use De Moivre's theorem, which should give ushow would you go about doing ci and cii?
View attachment 33594
Part b is quite easy as well all you have to do is let
Part c what is actually happening there is suppose we turn
part d is another elegent one. This part if you have learnt inequalities well you will be able to observe that
Last edited: