-
Looking for HSC notes and resources? Check out our Notes & Resources page 
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Australian Maths Competition (3 Viewers)
- Thread starter maths94
- Start date
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
Westpac Maths Comp marathon
okay, so the Westpac maths comp (aka AMC) is coming up so for those who are doing it or just want do some hard maths problems this "marathon" is a kind of warm up =)
So to get the ball rolling, i will post up a westpac maths question and who ever correctly solves it gets to post up another westpac question and then who ever solves that posts up another westpac question etc. We should start off fairly easy and increase the difficulty of the questions as the marathon progresses.
If you dont have any of the papers i have posted them here:
http://community.boredofstudies.org...australian-maths-competition.html#post4478693
Or if you have some of the questions from an earlier year feel free to post them =)
QUESTION 1
A rectangle has its length 25 times its width. What is the ratio of
its perimeter to the perimeter of the square of the same area?
-(A) 13 : 5 (B) 13 : 10 (C) 5 : 1 (D) 51 : 20 (E) 51 : 10
Ready, Steady, GO!
okay, so the Westpac maths comp (aka AMC) is coming up so for those who are doing it or just want do some hard maths problems this "marathon" is a kind of warm up =)
So to get the ball rolling, i will post up a westpac maths question and who ever correctly solves it gets to post up another westpac question and then who ever solves that posts up another westpac question etc. We should start off fairly easy and increase the difficulty of the questions as the marathon progresses.
If you dont have any of the papers i have posted them here:
http://community.boredofstudies.org...australian-maths-competition.html#post4478693
Or if you have some of the questions from an earlier year feel free to post them =)
QUESTION 1
A rectangle has its length 25 times its width. What is the ratio of
its perimeter to the perimeter of the square of the same area?
-(A) 13 : 5 (B) 13 : 10 (C) 5 : 1 (D) 51 : 20 (E) 51 : 10
Ready, Steady, GO!
d3st1nyLiang
Premium Member
- Joined
- Jan 23, 2009
- Messages
- 511
- Gender
- Male
- HSC
- 2011
Re: Westpac Maths Comp marathon
is it a)?
A lucky number is a positive integer which is 19 times the sum of its digits. How
many different lucky numbers are there?
is it a)?
A lucky number is a positive integer which is 19 times the sum of its digits. How
many different lucky numbers are there?
gurmies
Drover
Re: Westpac Maths Comp marathon
Yes, (a)
Yes, (a)
Re: Westpac Maths Comp marathon
By using the conditions in the questions. It's easy to deduce that the number isn't a 1,2 or 4 digit number. So it's a 3 digit no.
Let the digits be as follow: 100 digits in hundreds place, 10 digits in 10s place and 10 digits in 1's place.
Alternatively, I think you can just go:
Z*19=ABC where {Z,A,B,C E Z}
So say for: a no. which has digits summing to 6 is:
6*19=114
Thus, Z is in between 5 and 16
So 10 numbers.
I don't know if my methods right:is it a)?
A lucky number is a positive integer which is 19 times the sum of its digits. How
many different lucky numbers are there?
By using the conditions in the questions. It's easy to deduce that the number isn't a 1,2 or 4 digit number. So it's a 3 digit no.
Let the digits be as follow: 100 digits in hundreds place, 10 digits in 10s place and 10 digits in 1's place.
Alternatively, I think you can just go:
Z*19=ABC where {Z,A,B,C E Z}
So say for: a no. which has digits summing to 6 is:
6*19=114
Thus, Z is in between 5 and 16
So 10 numbers.
Last edited:
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
Re: Westpac Maths Comp marathon
Here is the solution:
As shaon showed, the lucky number must be a 3 digit number.
Suppose the number is abc.
Then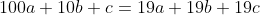 , we have:
, we have:

ie
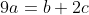
Note that as b and c are the ten's digit and unit's digit respectively, then
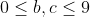
So the maximum) is
is ) and therefore the maximum a is
and therefore the maximum a is
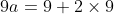
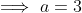
So we must only check for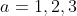
For a = 1, we have = (1, 4), (3,3), (5,2), (7,1), (9,0))
For a = 2, we have = (0, 9), (2,8), (4,7), (6,6), (8,5))
For a = 3, we have = (9, 9)) , and there are no other solutions.
, and there are no other solutions.
Hence there are exactly 11 lucky numbers, namely,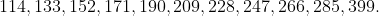
We should post up easier questions first just to get the marathon going =)
Close, the actual answer is 11 :|I don't know if my methods right:
By using the conditions in the questions. It's easy to deduce that the number isn't a 1,2 or 4 digit number. So it's a 3 digit no.
Let the digits be as follow: 100 digits in hundreds place, 10 digits in 10s place and 10 digits in 1's place.
Alternatively, I think you can just go:
Z*19=ABC where {Z,A,B,C E Z}
So say for: a no. which has digits summing to 6 is:
6*19=114
Thus, Z is in between 5 and 16
So 10 numbers.
Here is the solution:
As shaon showed, the lucky number must be a 3 digit number.
Suppose the number is abc.
Then
ie
Note that as b and c are the ten's digit and unit's digit respectively, then
So the maximum
So we must only check for
For a = 1, we have
For a = 2, we have
For a = 3, we have
Hence there are exactly 11 lucky numbers, namely,
We should post up easier questions first just to get the marathon going =)
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
Re: Westpac Maths Comp marathon
PROBLEM 3
Tina has a large number of 1 × 2 × 6 rectangular blocks. She wants
to make a solid cube out of the blocks. What is the smallest number
of blocks she needs?
(A) 6 (B) 12 (C) 18 (D) 36 (E) 144
PROBLEM 3
Tina has a large number of 1 × 2 × 6 rectangular blocks. She wants
to make a solid cube out of the blocks. What is the smallest number
of blocks she needs?
(A) 6 (B) 12 (C) 18 (D) 36 (E) 144
nerdsforever
hsc zomg
- Joined
- Jan 10, 2008
- Messages
- 464
- Gender
- Female
- HSC
- 2010
Re: Westpac Maths Comp marathon
or is it (c)?
or is it (c)?
Re: Westpac Maths Comp marathon
Yeah it is 11. lol. I counted my solutions in between 5 and 16 incorrectly.Close, the actual answer is 11 :|
Here is the solution:
As shaon showed, the lucky number must be a 3 digit number.
Suppose the number is abc.
Then, we have:
ie
Note that as b and c are the ten's digit and unit's digit respectively, then
So the maximumis
and therefore the maximum a is
So we must only check for
For a = 1, we have
For a = 2, we have
For a = 3, we have, and there are no other solutions.
Hence there are exactly 11 lucky numbers, namely,
We should post up easier questions first just to get the marathon going =)
Hi Kurt,Here is 2008 q + a and 2006 answers.
Thanks for these papers and answers for AMC. For some years there was just the answers and not teh solution methods as such. Can you send these also if you have, say for 2008, 2006,2005,2004 and 2003? I am taking part inthe JUnior level. Thanks.
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
Re: Westpac Maths Comp marathon
Here my solution:
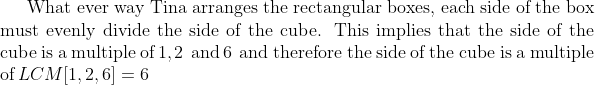
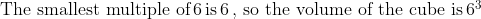
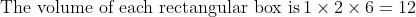

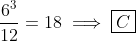
Yes, the answer is (c)or is it (c)?
Here my solution:
Aquawhite
Retiring
I think I am meant to be in this >_>... I'm really not in the mood for doing this since the Trials are just around the corner and all I've focused on is the syllabus and not really extra curricular (interesting maths ...).
Ima probably end up with just a participation or a credit if I'm lucky probably. Not that I care XD
Ima probably end up with just a participation or a credit if I'm lucky probably. Not that I care XD
9876543210
everything's fuzzy..
thx kurt!
nerdsforever
hsc zomg
- Joined
- Jan 10, 2008
- Messages
- 464
- Gender
- Female
- HSC
- 2010
Re: Westpac Maths Comp marathon
Cheers kurt! you're awesome. what do you usually get in the maths comp?
Here's a new question.
A sequence {u1, u2, . . . , un} of real numbers is defined by
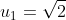
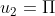
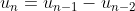 for n≥ 3.
for n≥ 3.
What is u2008?
(A) −√2
(B) 2008(√2 − 2008pi)
(C) 1003√2 − 1004pi
(D) pi
(E)√2
Cheers kurt! you're awesome. what do you usually get in the maths comp?
Here's a new question.
A sequence {u1, u2, . . . , un} of real numbers is defined by
What is u2008?
(A) −√2
(B) 2008(√2 − 2008pi)
(C) 1003√2 − 1004pi
(D) pi
(E)√2
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
Re: Westpac Maths Comp marathon
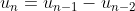
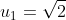
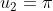
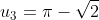
 - \pi = - \sqrt{2})
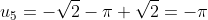
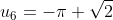
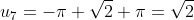
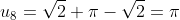
We see the pattern emerging s.t.
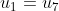
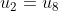
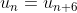
So consider the pattern in modulo 6.
The 2008th term will be equivalent a specific residue modulo 6 and hence we can determine which term the 2008th term is equivalent to
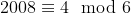
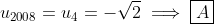
Cheers kurt! you're awesome. what do you usually get in the maths comp?
Here's a new question.
A sequence {u1, u2, . . . , un} of real numbers is defined by
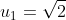
for n≥ 3.
What is u2008?
(A) −√2
(B) 2008(√2 − 2008pi)
(C) 1003√2 − 1004pi
(D) pi
(E)√2
We see the pattern emerging s.t.
So consider the pattern in modulo 6.
The 2008th term will be equivalent a specific residue modulo 6 and hence we can determine which term the 2008th term is equivalent to
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
Re: Westpac Maths Comp marathon
Problem 5
The sum of three numbers is 4, the sum of their squares is 10 and the sum of their
cubes is 22. What is the sum of their fourth powers?
Problem 5
The sum of three numbers is 4, the sum of their squares is 10 and the sum of their
cubes is 22. What is the sum of their fourth powers?
kurt.physics
Member
- Joined
- Jun 16, 2007
- Messages
- 823
- Gender
- Undisclosed
- HSC
- N/A
I re-found the website which has the papers =)
AMC papers (this is in Chinese ;P)
AMC papers (in English)
(for the second link you have to click on the "Downloads" tab to the left)
AMC papers (this is in Chinese ;P)
AMC papers (in English)
(for the second link you have to click on the "Downloads" tab to the left)
Last edited:
appl3licious
New Member
- Joined
- Aug 4, 2009
- Messages
- 5
- Gender
- Female
- HSC
- 2012
Australian Mathematics Competition
Hi everyone~
i was just wondering if anyone had the AMT solutions for year 2002 - 2006 (intermediate division)???
Hi everyone~
i was just wondering if anyone had the AMT solutions for year 2002 - 2006 (intermediate division)???
