Cambridge Prelim MX1 Textbook Marathon/Q&A (2 Viewers)

drsabz101 · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

also this question:

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

drsabz101 said:
What steps do I take to solve this?
View attachment 32956

$$ EX 7G Part 10 (c) $ \frac{dy}{dx}=\frac{1}{(x+1)^2}$

$At x=1, \frac{dy}{dx}=\frac{1}{(1+1)^2}= \frac{1}{4}$

$y-y_{1}=m(x-x_{1})$

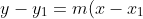$$ The coordinate is $ A(1,\frac{1}{2}) $ and gradient is $ \frac{1}{4}$

$y-\frac{1}{2}=\frac{1}{4}(x-1)$

$$ Rearranging gives, $ y=\frac{x}{4}+\frac{1}{4}$

$Bisect means to divide into two equal parts. You can bisect lines, angles and more. The dividing line is called the 'bisector'. In this case from (-1,0) to the Origin, is equal in distance from the Origin to (1,0)$

InteGrand · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

drsabz101 said:
also this question:

View attachment 32957

$\noindent For the first one, $xy = u$. Then differentiate both sides with respect to $x$ (use the product rule for the L.H.S.).$

$\noindent For the second one, $uy=x$. Then differentiate both sides with respect to $x$ (use the product rule for the L.H.S.).$

drsabz101 · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

okay thankyou, I'll do it now

drsabz101 · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

when u differentiate xy=u

do u differentiate "xy" first using product rule:

I got y'=u/u^2

drsabz101 · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

ohh wait i let v=u not v=y

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

drsabz101 said:
when u differentiate xy=u

do u differentiate "xy" first using product rule:

I got y'=u/u^2

$Exercise 7G Q 11 (a) Not sure if you have learnt it this way by I use the Product Rule \ Implicit Differentiation$

$xy=u , by Using the product rule break up the x and y terms into 2 parts$

$\frac{d}{dx} (x) \times y +\frac{d}{dx} (y) \times x = \frac{du}{dx}$

$(1)y+x \frac{dy}{dx}=\frac{du}{dx}$

$y+x \frac{dy}{dx}=\frac{du}{dx}$

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

$$ Exercise 7G Q 11 (b)$

$uy=x$

$y \frac{d}{dx} (u) + u \frac{d}{dx} (y) = 1$

$y \frac{du}{dx} + u \frac{dy}{dx} = 1$

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

Anyone have any idea on Exercise 7G, Q 10 d? I've had a couple of attempts at this question but I'm thinking of substituting c=10 and c=-5 as an examples to show the proof for (i) and (ii)

InteGrand · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

davidgoes4wce said:
Anyone have any idea on Exercise 7G, Q 10 d? I've had a couple of attempts at this question but I'm thinking of substituting c=10 and c=-5 as an examples to show the proof for (i) and (ii)

What is the question?

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

InteGrand said:
What is the question?

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

OK this is my thinking. 'A tangent line' is defined as a straight line that touches a function at only one point.

If we visualise is :

No matter where you draw a linear line from the Point (3,0), the straight line will always have multiple points of intersection. So that rules out c>0, having no tangents passing through (c). ( A Vertical Line is not any good for us because that is an undefined value)

Nailgun · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

davidgoes4wce said:
OK this is my thinking. 'A tangent line' is defined as a straight line that touches a function at only one point.

If we visualise is :

No matter where you draw a linear line from the Point (3,0), the straight line will always have multiple points of intersection. So that rules out c>0, having no tangents passing through (c). ( A Vertical Line is not any good for us because that is an undefined value)

What about a horizontal line?
(I haven't actually tried the question lol)

InteGrand · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

davidgoes4wce said:
OK this is my thinking. 'A tangent line' is defined as a straight line that touches a function at only one point.

If we visualise is :

No matter where you draw a linear line from the Point (3,0), the straight line will always have multiple points of intersection. So that rules out c>0, having no tangents passing through (c). ( A Vertical Line is not any good for us because that is an undefined value)

A tangent line doesn't need to only touch the curve once. It needs to share the same point at some point on the curve, and also match the slope there, where the slope is the value of the derivative there (assuming the slope isn't infinite there).

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

InteGrand said:
A tangent line doesn't need to only touch the curve once. It needs to share the same point at some point on the curve, and also match the slope there, where the slope is the value of the derivative there (assuming the slope isn't infinite there).

I just quickly read up on it here:

http://clas.sa.ucsb.edu/staff/lee/secant, tangent, and derivatives.htm

But you are right about the slope of the value of the derivative there.

Paradoxica · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

InteGrand said:
A tangent line doesn't need to only touch the curve once. It needs to share the same point at some point on the curve, and also match the slope there, where the slope is the value of the derivative there (assuming the slope isn't infinite there).

Technically it's still a tangent when it's vertical.

InteGrand · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

davidgoes4wce said:

$\noindent To do the question you were asking about, recall that we found the equation of the tangent to the curve at $x=a$ earlier. Using this equation, the point $(c,0)$ lies on a tangent if and only if there exists $a$ in the domain of the function such that $c-(a+1)^2\cdot 0 +a^2 = 0\Longleftrightarrow c = -a^2$. Now if $c>0$, there is clearly no such $a$, since $-a^2 \leq 0$ for real $a$. If $c<0$ and $c\neq -1$, then $c = -a^2$, so $a = \pm \sqrt{-c}$, where this is well defined and real, since $-c>0$, and $c\neq -1$, so neither of these $a$-values are $-1$ (which would be a problem if they were, since $-1$ isn't in the function's domain). So the places on the curve have $x$-values that are opposite of each other.$

$\noindent You can now try doing the last part of the question.$

InteGrand · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

Paradoxica said:
Technically it's still a tangent when it's vertical.

I know. It's just then we shouldn't say it's the value of the derivative there, since the derivative would technically be undefined there.

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

Something has just rung a bell to me. Referring back to part (b)

$If we substitute (c,0) into the equation , c-(a+1)^2 (0) +a^2=0 \implies c+a^2=0 \implies c=-a^2$

$Since $ c=-a^2. $ No matter what value of ' a' we substitute, it will always return a negative c value.$

$$ If we substitute (-c,0) into the equation, we get $ -c=-a^2 \implies c=a^2 \implies c=+\sqrt{a} \ $ and $ c=-\sqrt{a}$

$Hence, if c is a negative value by taking the square roots we get the 2 solutions , which gives us the two tangents through T whose x-coordinates of their points of contact are opposites of each other.$

davidgoes4wce · Feb 28, 2016

Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread

$Answer from the back of the book : Substitute (c,0) then c+a^2=0 $ , so \ a=-\sqrt{c} \ or \ \sqrt{-c}. For -1<c<0, $ they are both on the right-hand branch. $ For \ c < -1, $ they are both on the right hand branch. $ For c<-1, $ they are on different branches.$

Cambridge Prelim MX1 Textbook Marathon/Q&A (2 Viewers)

Member

Well-Known Member

Well-Known Member

Member

Member

Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Cole World

Well-Known Member

Well-Known Member

-insert title here-

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 2)