Aysce
Well-Known Member
- Joined
- Jun 24, 2011
- Messages
- 2,394
- Gender
- Male
- HSC
- 2012
Question: (Note I've done the first part)
10.a. Prove that the points on an Argand diagram which represent the complex numbers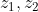 and
and 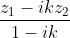 where k is a real number, form the vertices of a right angled triangle. You may assume the right angle is at the point
where k is a real number, form the vertices of a right angled triangle. You may assume the right angle is at the point 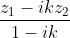 .
.
b. For what values of k is the above triangle an isosceles right-angled triangle?
This question is from Terry Lee and do they happen to ask these sort of questions in HSC or trial papers?
10.a. Prove that the points on an Argand diagram which represent the complex numbers
b. For what values of k is the above triangle an isosceles right-angled triangle?
This question is from Terry Lee and do they happen to ask these sort of questions in HSC or trial papers?

