You know that
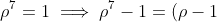\left(1 + \rho + \rho^2 + \rho^3 + \rho^4 + \rho^5 + \rho^6\right)=0)
, which solves (a) as
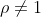
With
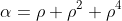
and wanting a quadratic with real coefficients, our second root must be the conjugate of

, which is
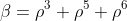
. We then have
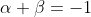
and
\left(\rho^3 + \rho^5 + \rho^6\right) \\ &= \rho^4\left(1 + \rho + \rho^3\right)\left(1 + \rho^2 + \rho^3\right) \\ &= \rho^4\left(1 + \rho^2 + \rho^3 + \rho + \rho^3 + \rho^4 + \rho^3 + \rho^5 + \rho^6\right) \\ &= \rho^4\left(1 + \rho + \rho^2 + 3\rho^3 + \rho^4 + \rho^5 + \rho^6\right) \\ &= \rho^4\left(0 + 2\rho^3\right) \\ &= 2\rho^7 \\ &= 2 \end{align*})
and thus our quadratic is
x + \alpha\beta = x^2 + x + 2)
which has solutions
(2)}}{2(1)}=\frac{-1\pm i\sqrt{7}}{2})
Looking at the result in the last part, it appears we need the imaginary part of one of the roots.
}&=\Im{\left(\rho+\rho^2+\rho^4\right)} \\ &=\Im{\left(\rho\right)}+\Im{\left(\rho^2\right)}+\Im{\left(\rho^4\right)} \\ &=\sin{\frac{2\pi}{7}}+\sin{\frac{4\pi}{7}}+\sin{\frac{8\pi}{7}} \\ &=\sin{\frac{2\pi}{7}}+\sin{\left(\pi-\frac{4\pi}{7}\right)}+\sin{\left(\pi-\frac{8\pi}{7}\right)} \qquad \text{as $\sin{\left(\pi-\theta\right)}=\sin\theta$} \\ &=\sin{\frac{2\pi}{7}}+\sin{\frac{3\pi}{7}}+\sin{\frac{-\pi}{7}} \\ &=\sin{\frac{2\pi}{7}}+\sin{\frac{3\pi}{7}}-\sin{\frac{\pi}{7}} \qquad \text{as $\sin\theta$ is an odd function and so $\sin{-\theta}=-\sin\theta$} \\ &= -\sin{\frac{\pi}{7}}+\sin{\frac{2\pi}{7}}+\sin{\frac{3\pi}{7}} \end{align*})
}&=\Im{\left(\rho^3+\rho^5+\rho^6\right)} \\ &=\Im{\left(\rho^3\right)}+\Im{\left(\rho^5\right)}+\Im{\left(\rho^6\right)} \\ &=\sin{\frac{6\pi}{7}}+\sin{\frac{10\pi}{7}}+\sin{\frac{12\pi}{7}} \\ &=\sin{\left(\pi-\frac{6\pi}{7}\right)}+\sin{\left(\pi-\frac{10\pi}{7}\right)}+\sin{\left(\pi-\frac{12\pi}{7}\right)} \qquad \text{as $\sin{\left(\pi-\theta\right)}=\sin\theta$} \\ &=\sin{\frac{\pi}{7}}+\sin{\frac{-3\pi}{7}}+\sin{\frac{-5\pi}{7}} \\ &=\sin{\frac{\pi}{7}}-\sin{\frac{3\pi}{7}}-\sin{\frac{5\pi}{7}} \qquad \text{as $\sin\theta$ is an odd function and so $\sin{-\theta}=-\sin\theta$} \\ &=\sin{\frac{\pi}{7}}-\sin{\frac{3\pi}{7}}-\sin{\left(\pi-\frac{5\pi}{7}\right)} \\ &=-\left(-\sin{\frac{\pi}{7}}+\sin{\frac{2\pi}{7}}+\sin{\frac{3\pi}{7}}\right) \end{align*})
Now, we know that, on
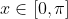
, the function
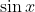
increases from 0 to a maximum of 1 (occurring when
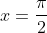
) and then decreases back to 0. We therefore know that:
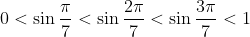
and thus that
}=-\sin{\frac{\pi}{7}}+\sin{\frac{2\pi}{7}}+\sin{\frac{3\pi}{7}}> 0)
and that
}=\sin{\frac{\pi}{7}}-\sin{\frac{2\pi}{7}}-\sin{\frac{3\pi}{7}}< 0)
and so we can conclude that
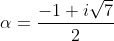
and
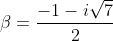
and by equating the imaginary parts of either

or
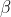
, we get
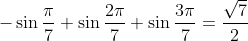
---
Note, we can get other identities by means such as putting
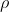
into the expression from (a), and taking the real part, to give:
 = \cos\theta$} \\ \cos{\frac{2\pi}{7}} + \cos{\frac{4\pi}{7}} + \cos{\frac{6\pi}{7}} &= -\frac{1}{2} \\ \cos{\frac{2\pi}{7}} - \cos{\frac{3\pi}{7}} - \cos{\frac{\pi}{7}} &= -\frac{1}{2} \quad \text{since $\cos(\pi-\theta) = -\cos\theta$} \\ \cos{\frac{\pi}{7}} - \cos{\frac{2\pi}{7}} + \cos{\frac{3\pi}{7}} &= \frac{1}{2} \end{align*})