RohitShubesh21
New Member
- Joined
- Oct 21, 2021
- Messages
- 18
- Gender
- Male
- HSC
- 2024
Yes I am done that but I am not getting answer I think my argument is wrong. I have got pi/6 but when I add 2kpi it is getting wrong answer.You can go about it by converting it into polar form, so you can equate the equation above to cos(theta) + i*sin(theta). Then, getting the right modulus and argument, you can graph the roots on a diagram
As the Cartesian equation has 2 negatives, the argument should lie in the 4th quadrant. Thus, your argument should be a negative, acute angle.Yes I am done that but I am not getting answer I think my argument is wrong. I have got pi/6 but when I add 2kpi it is getting wrong answer.
I think you mean the third quadrant...As the Cartesian equation has 2 negatives, the argument should lie in the 4th quadrant. Thus, your argument should be a negative, acute angle.
Oh yep, my bad. I accidentally referenced the bottom right quadrant as the 1st quadrant instead of the top rightI think you mean the third quadrant...
yea I thought I was smart when I was the only person who could recite the quadratic formula by heart in year 9year 9s already starting complex
now that's dedication
i thought i was smart when i could multiply fractions in kindyyea I thought I was smart when I was the only person who could recite the quadratic formula by heart in year 9
Hahah lol same I guess notyea I thought I was smart when I was the only person who could recite the quadratic formula by heart in year 9
alternatively,Expand the RHS from (b), which is equal to, to get the values for
and
These are the values ofand
, the roots of the quadratic
with the desired roots.
You should get thatfor
a non-zero constant.
Sorry I dont understand yet. Could you do working out so I can see how to do... sorry verymuch
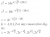
Thank you sir,... I am asumming the identity z^n + z^-n = 2cosnt .. is it assumed or I need to prove sir?.alternatively,
1+z+z^2+z^3+z^4 = 0
(z^2+z^-2) + (z+z^-1) + 1 = 0
2cos2t + 2cost + 1 = 0
4cos^2t + 2cost - 1 = 0
Let cost = x,
hence 4x^2+2x-1 = 0 for Re(z), where z=/1, z is a 5th root of unity, which is cos2pi/5, cos4pi/5.
Ohok, thanks very muchsir.View attachment 32881
Now you would get the angle to be pi/3 when you do tan^1(-8sqrt(3)/-8) however that does not necessarily mean that the argument is pi/3. Construct a diagram and plot the complex number, you will find it lies on the 3rd quadrant. What you are doing with tan^1(-8sqrt(3)/-8) is you are finding the angle of that triangle specifically in that quadrant, not the actual argument itself. Hence the argument would be -2pi/3 when you do pi - pi/3. I believe this is the error you made - everything else is just routine.
Drawing it up is pretty straightforward, if you do need a diagram feel free to ask. Also its commendable that you have started this topic at Year 9 already, and you have the initiative to do so! Don't feel shy to ask for more help in the forums as I'm sure more people will be willing to help out. Welcome.
prove it if you want to play it safe.Thank you sir,... I am asumming the identity z^n + z^-n = 2cosnt .. is it assumed or I need to prove sir?.
If you were just to assert it, make sure you note that it is only true if |z| = 1, and show that condition is satisfied in the circumstances in which you use it.Thank you sir,... I am asumming the identity z^n + z^-n = 2cosnt .. is it assumed or I need to prove sir?.
