kingkong123
Member
- Joined
- Dec 20, 2011
- Messages
- 98
- Gender
- Male
- HSC
- 2012
Hey guys i need help with this question:
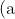 Show that the equation } x^{3}-6x^{2}+9x-5 = 0 \textup{ has only one real root } \alpha. \\ \textup{(b) Determine the two consecutive integers between which } \alpha \textup{ lies.} \\\textup{(c) By considering the product of the roots of the equation express the modulus of each of the complex roots in terms of } \alpha\\\textup{ and deduce that the value of this modulus lies between }1\textup{ and }\frac{\sqrt{5}}{2})
What ive done so far is for part (i) I showed that the stationary points are both under the x-axis (simply by finding P'(x)=0 and subbing back into P(x)). I then proved one is a relative max and the other a relative min (by testing P''(x)). Hence there must only be one real solution with the other solutions occurring in a conjugate pair due to real co-effs. I need help finding the values which
with the other solutions occurring in a conjugate pair due to real co-effs. I need help finding the values which  lies between.
lies between.
For part (iii) i let the roots be . Then using product of roots i got
. Then using product of roots i got  but
but  , therefore
, therefore  . I need help getting the values for which the modulus lies.
. I need help getting the values for which the modulus lies.
Also any comments on my method? Any easier method??
Thanks in advance!!
What ive done so far is for part (i) I showed that the stationary points are both under the x-axis (simply by finding P'(x)=0 and subbing back into P(x)). I then proved one is a relative max and the other a relative min (by testing P''(x)). Hence there must only be one real solution
For part (iii) i let the roots be
Also any comments on my method? Any easier method??
Thanks in advance!!
