I'm not very experienced with modulo and congruency, but using the 4 properties that I do know:




I've named the properties respectively:
First, we notice by inspection that:

And since by (3), we can multiply the congruencies side by side, simply multiply them side by side 59 times:

Now, we also notice that:

Multiply 87 of these side by side (by property (3))

Now, notice that:

Multiply side by side by property (3)

Now my property (1)

So we now have 3 congruencies:



Add them side by side by property (2):

Translate this into the fact that:

Says that (a-b)/m is an integer, so:
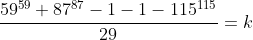
(*)
for integer k.
We are looking for some r integer where of the form:

Rearranging (*), we find that the remainder is 2.
(I hope this is right)

