namelyanonymous
Member
The question is (Question 9 from Fitz. 4 Unit 32(c)):
"P is a variable point on the ellipse with equation:
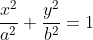
and S and S' are the focii. Show that PS and PS' are equally inclined to the tangent at P."
I have no idea what I'm trying to prove. What does it mean by "equally inclined"? If we're looking at perpendicular distance to the tangent, then isn't it obvious that they'd both have the same angle towards the tangent relative to the horizontal as they're both just points? Or am I looking at it the wrong way?
"P is a variable point on the ellipse with equation:
and S and S' are the focii. Show that PS and PS' are equally inclined to the tangent at P."
I have no idea what I'm trying to prove. What does it mean by "equally inclined"? If we're looking at perpendicular distance to the tangent, then isn't it obvious that they'd both have the same angle towards the tangent relative to the horizontal as they're both just points? Or am I looking at it the wrong way?
Last edited:

