asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
Just a question

Why are there inflexion points there and there?
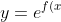}\\y'=f'(x)e^{f(x)}\\y''=f'(x)f'(x)e^{f(x)}+e^{f(x)}f''(x)=e^{f(x)}\left[(f'(x))^2+f''(x)\right]=0 $ for points of inflexion.$) But neither the function nor the exponential have inflexion points??
But neither the function nor the exponential have inflexion points??
Also what's the relevance of y=-1?
Thanks
Why are there inflexion points there and there?
Also what's the relevance of y=-1?
Thanks
Attachments
-
89.6 KB Views: 168
Last edited:

