1)
Straight away this integral must be negative, so the answer is either A or D.
)
appears to be symmetric around the y-axis, so
\, dx = 2 \int _{0}^2 f(x)\, dx )
You are given
+g(x)\, dx = \int _0^2 f(x)\, dx+\int _0^2g(x)\, dx = \pi - 10)
and note that
\, dx )
represents the area of the semicircle from 0 to 2, which you can find in exact form.
2)
)
A quadratic is positive definite (i.e. always greater than zero) if:
- it has no real roots, and
- its leading coefficient is positive.
(It's easy to visualise this by thinking of a quadratic as a parabola on a graph)
This restriction on the leading coefficient (
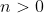
) eliminates two of the possible answers immediately.
You can do a simple substitution test on the remaining two choices, which are
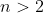
and
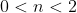
.
If the quadratic is positive for all values of
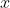
, it must be positive for
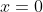
. Substituting
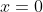
, we are left with just the constant term
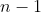
, which has to be positive.
3)
i) If you haven't already, use Simpson's rule. I like to remember it as
\, dx \approx \frac{h}{3}[2(y_1+y_3+y_5 +...) + 4(y_2 +y_4+y_6 +...)] )
Where
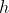
is the interval length.
ii) A diagram really helps to understand the problem.
Every second, 1.8m of water passes through the cross section.
You can imagine a 3D prism 1.8m long, whose cross section is that of the river's. That's how much water passes through every second.
So, the volume of water passing through the cross section each second is given by
\left( \int f(x) \, dx\,\mathrm{m^2}\right) = \left( 1.8 \int f(x) \, dx\,\right) \mathrm{m^3/s})
And to get the amount in 2 hours, just do another multiplication.