Re: MATH1131 help thread
, we will have: $\overrightarrow{OG}=\overrightarrow{EF}$ (because opposite sides of a parallelogram are equal in length and parallel, so those vectors are equal). This means that $\vec{g} = \vec{f}-\vec{e}$. Since we are given $\vec{e}$ and $\vec{f}$, we can calculate $\vec{g}$.$)
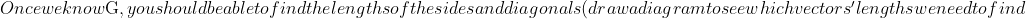.$)

Stuck on this for 30mins. Help would be appreciated
Last edited:

Stuck on this for 30mins. Help would be appreciated
Find a vector with a magnitude of 10 which is parallel to u. u = <2,1,7>.
*I know the answer, don't know how to get there.
Thanks
thanks man!
A=[-1,3;2,2;4,1]Sorry I had a typo on the first point D:
Answers say 'yes' .
Since the two vectors are parallel, their components are in the same ratio, so
this is probably really simple: they are vectors
Haha liking the LaTeX (y)
this is probably really simple: they are vectors
OH. SCALAR PRODUCT!Haha liking the LaTeX (y)
(Yeah just remember that two parallel vectors are scalar multiples of each other)
I edited already lol. I realised.It's not really scalar "product" (the term "scalar product" commonly refers to the dot product). Better to say scalar "multiple".
TRUUIt's not really scalar "product" (the term "scalar product" commonly refers to the dot product). Better to say scalar "multiple".
If you're just showing that it has a zero you can pick any arbitrary interval. We just care that you know to pick one that conveniently has one side negative and the other positive.How do I know what interval to use for this question (I get how to use it after that)?
x^3 + root(3)x - 6
use intermediate value theorem to prove that f has at least one real root
Yes that's what I'm asking how do I do that?If you're just showing that it has a zero you can pick any arbitrary interval. We just care that you know to pick one that conveniently has one side negative and the other positive.
Oh and of course it's continuous on that interval as well.
That's not even hard. Just put random numbers (for x) into your calculator and get something >0 and something <0 ?Yes that's what I'm asking how do I do that?
