Pointing out that questions of this type (even if they involved no complex numbers) cannot be asked in the Extension 1 course.
The following question was asked on the 1992 Sydney Grammar 4u trial:
Consider the sequence defined by
(i) Determine the values of
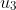
and
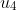
.
(ii) Show that
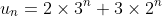
for
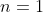 and
and 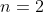
.
(iii) If
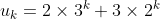 and
and 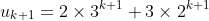
, where

is a positive integer, prove that
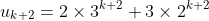
.
(iv) What conclusion may be reached as a result of parts (ii) and (iii)?
A question like this requires use of algebra and index laws. The conclusion in part (iv) uses the logic of induction but the response is simply that the general formula
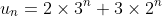
is true for all positive integers

, and thus allows any member of the sequence to be determined. I can argue that the question is not an induction question, especially if part (iv) is excluded. The question could be extended to summing the series
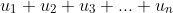
by splitting it into two GPs, making the topic sequences and series.
My point is that the syllabus may not allow a particular question in a particular form, but that doesn't mean the same content can't be examined by restructuring a question. A determined examiner can certainly bend the syllabus in places - not so far as breaking it (which using complex numbers would do for MX1) - but enough that I think paying a lot of attention to what is and is not "allowed" is unwise, especially for students who may be unaware of some subtleties. Predicting boundaries is also problematic for trials and internal papers where the scrutiny given in preparation is less stringent.
Another example: many MX1 students were convinced that binomial theorem questions wouldn't appear in the HSC as preliminary materials, but the 2020 HSC proved that to be incorrect. Any preliminary materials can be covered if they are part of a question on HSC course content.
View attachment 30516
