Toloza's formula can be generalised to relate π to every second diagonal of Pascal's triangle
When you learned trig did you ever use these archaic trig functions?
Versine: versin(θ)=1-cos(θ)
Vercosine: vercosin(θ)=1+cos(θ)
Coversine: coversin(θ)=1-sin(θ)
Covercosine: covercosine(θ)=1+sin(θ)
Haversine: haversin(θ)=versin(θ)/2
Havercosine: havercosin(θ)=vercosin(θ)/2
Hacoversine: hacoversin(θ)=coversin(θ)/2
Hacovercosine: hacovercosin(θ)=covercosin(θ)/2
Exsecant: exsec(θ)=sec(θ)-1
Excosecant: excsc(θ)=csc(θ)-1
It means the formula for
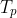
is actually a sum of excosecants.
So it could also be written as
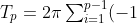^{i-1}{2p-2\choose i-1}\text{excsc}\frac{\pi i}{2p})




