-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Higher Level Integration Marathon & Questions (1 Viewer)
- Thread starter leehuan
- Start date
Last edited:
Re: Extracurricular Integration Marathon
 e^{-t} \cos t \right )^\infty_0 - \int^\infty_0 n \tan^{-1} (n t) d(e^{-t} \cos t) \, dt \right ]\,\,\, \mbox{(using IBP)}\\&= -\lim_{n \rightarrow \infty} \int^\infty_0 \tan^{-1} (nt) d(e^{-t} \cos t) \, dt\\&= -\int^\infty_0 \left [\lim_{n \rightarrow \infty} \tan^{-1} (nt) \right ] d(e^{-t} \cos t) \, dt\\&= -\frac{\pi}{2} \int^\infty_0 d(e^{-t} \cos t) \, dt\\&= -\frac{\pi}{2} \left [e^{-t} \cos t \right ]^\infty_0\\&=\frac{\pi}{2}\end{align*})
Here's another nice question.

Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
 But my solution involved factorising out the 1/4 so basel's could be seen easily. But my main problem is that I can't get rid of the negative that appears in the series expansion for log(1-x). Here's my solution, which ignores the sign error...
But my solution involved factorising out the 1/4 so basel's could be seen easily. But my main problem is that I can't get rid of the negative that appears in the series expansion for log(1-x). Here's my solution, which ignores the sign error...
} $d$x \\ 4I = \int _0^{\frac{\pi}{2}} \frac{2\sin{x}\cos{x}}{\sin^2{x}} \log{(1-\sin^2{x})} $d$x = \int _0^1 \frac{1}{v}\log{(1-v)}$d$v \\ 4I = \int_0^1 \sum_{r=1}^\infty \frac{v^{r-1}}{r} $d$v = \sum_{r=1}^\infty \int_0^1 \frac{v^{r-1}}{r} $d$v = \sum_{r=1}^\infty \frac{1}{r^2} = \zeta(2) \\ I = \frac{\pi^2}{24})
WHERE DID THE MISSING SIGN GO?!?!?!
Beat me to it by nine hours
WHERE DID THE MISSING SIGN GO?!?!?!
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: Extracurricular Integration Marathon

= \frac{1}{\pi}\int_0^{\pi}{(x+i\sqrt{1-x^2}\cos{\theta})^n}d\theta )
| \leq 1 )
Re: Extracurricular Integration Marathon
$ in the integrand, but the original integral had $\sec$, not $\cos$, so you need to put in a minus sign in your first line to make it equal a $\ln (\sec x)$, as $\ln (\sec x) =-\ln (\cos x)$.$)
Beat me to it by nine hoursBut my solution involved factorising out the 1/4 so basel's could be seen easily. But my main problem is that I can't get rid of the negative that appears in the series expansion for log(1-x). Here's my solution, which ignores the sign error...
WHERE DID THE MISSING SIGN GO?!?!?!
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
I hope that's what you meant by inequality, because olympiad inequalities don't look any more viable than brute force.
Minkowski Inequality easily destroys the odd valued cases, but is itself destroyed by the even valued cases.
I hope that's what you meant by inequality, because olympiad inequalities don't look any more viable than brute force.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
The triangle inequality completes the proof.
The integrand has its modulus squared equal to (x^2 + (1-x^2)cos^2(theta))^n =< (x^2 + (1-x^2))^n=1.
The triangle inequality completes the proof.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
The Laurent series for arctan(z) looks unpromising.... We need a different approach.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: Extracurricular Integration Marathon
When we do Cauchy's Integrals what are we supposed to picture in our heads?
When we do Cauchy's Integrals what are we supposed to picture in our heads?
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
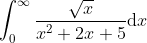
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: Extracurricular Integration Marathon
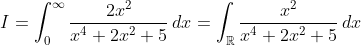
This integral is clearly a prime target for contour integration. (We could factorise into its real quadratic factors, use partial fractions, and integrate the simpler summands, but contour integration seems faster).
Note that since the quartic denominator is both even and real, the poles of the integrand occur at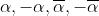 where
where  is an arbitrarily chosen root, say the one in the first quadrant of the the complex plane.
is an arbitrarily chosen root, say the one in the first quadrant of the the complex plane.
Now if we take a semicircular contour (radius R) with diameter on the real axis centred at the origin, and semicircular arc in the upper half-plane, then the integral around this contour (with positive orientation) is just equal to I, because the integrand decays as 1/R^2, and so the contribution from the curved segment of length O(R) tends to zero.
On the other hand, for sufficiently large R this integral is just equal to

It remains to compute , which is just the principal square root of
, which is just the principal square root of 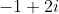 .
.
Writing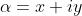 , we get
, we get 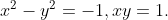
The resulting biquadratic yields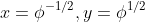 , where
, where 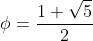 is the golden ratio.
is the golden ratio.
Hence
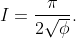
This integral is clearly a prime target for contour integration. (We could factorise into its real quadratic factors, use partial fractions, and integrate the simpler summands, but contour integration seems faster).
Note that since the quartic denominator is both even and real, the poles of the integrand occur at
Now if we take a semicircular contour (radius R) with diameter on the real axis centred at the origin, and semicircular arc in the upper half-plane, then the integral around this contour (with positive orientation) is just equal to I, because the integrand decays as 1/R^2, and so the contribution from the curved segment of length O(R) tends to zero.
On the other hand, for sufficiently large R this integral is just equal to
It remains to compute
Writing
The resulting biquadratic yields
Hence
Last edited:
Paradoxica
-insert title here-
Last edited:
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
\ln^2{(x+1)}}{(4x^2 +8x +5)^{\frac{3}{2}}}\,$d$x)
Paradoxica
-insert title here-
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: Extracurricular Integration Marathon

