-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Horizontal asymptote HELP (1 Viewer)
- Thread starter Triage
- Start date
Timske
Sequential
- Joined
- Nov 23, 2011
- Messages
- 794
- Gender
- Male
- HSC
- 2012
- Uni Grad
- 2016
^ vertical asymptote,so the highest power of x in the denominator is 1, since its just x
f(x) =[ (5/x)-1 ]/ [(4/x)-2]
then the limit is as x approaches infinity 5/x and 4/x become 0, so the asymptote will be -1/-2 = 2
4-2x =/= 0
-2x =/= -4
x =/= 2
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Ok since I cant find that long post on asymptotes I made, Ill give a brief explanation:
Take our function:
=\frac{ax+k}{bx+m} )
The horizontal asymptote will be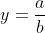
And this can be derived from mere observation as well. Take any very large values of x, k and m are really insignificant.
Now we have in the numerator a multiplied by our very large number, in denominator, b multiplied by very large number.
These very large numbers 'cancel' out and then we are left with a/b
For functions such as:
=\frac{1}{ax+k} )
Horizontal asymptote will always be zero, since the denominator will largely dominate the numerator (in terms of value). Hence it comes to 0.
For the question you posted:
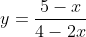
Our 'a' is -1, and our 'b' is -2
Hence our horizontal asymptote is y=0.5
You can find horizontal asymptotes by subbing in very large (or very small) values of x on your calculator, and see where they are coming close to
Take our function:
The horizontal asymptote will be
And this can be derived from mere observation as well. Take any very large values of x, k and m are really insignificant.
Now we have in the numerator a multiplied by our very large number, in denominator, b multiplied by very large number.
These very large numbers 'cancel' out and then we are left with a/b
For functions such as:
Horizontal asymptote will always be zero, since the denominator will largely dominate the numerator (in terms of value). Hence it comes to 0.
For the question you posted:
Our 'a' is -1, and our 'b' is -2
Hence our horizontal asymptote is y=0.5
You can find horizontal asymptotes by subbing in very large (or very small) values of x on your calculator, and see where they are coming close to
zeebobDD
Member
- Joined
- Oct 23, 2011
- Messages
- 411
- Gender
- Male
- HSC
- 2012
no it's not thats the horizontal.... i was right except -1/-2 =/= 2 it equals half LOL^ vertical asymptote,
4-2x =/= 0
-2x =/= -4
x =/= 2
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,419
- Gender
- Male
- HSC
- N/A
You divide by the highest power of x, then you take the limit as x approaches infinity.This may be an easy question but I just cannot understand the explanation.
Find the horizontal asymptote of these functions by dividing through by the highest power of x in the denominator.
F(x) = (5-x)/(4-2x)
Cheers
The highest power of x is x1, so you divide each term by x1. If the highest power was a square (2), then you divide through each term by x2.
Then you recognise as x approaches infinity, 1/x approaches 0 (zero), so you can then simplify it like so.
Last edited:
