RealiseNothing
what is that?It is Cowpea
Re: HSC 2012 Marathon 
Now we show that the derivatives are also equal as the functions approach x=0.
It is trivial that the derivative of 0 is 0 as x approaches 0.
Now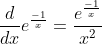
As x approaches 0, the 'e' will dominate the 'x'. So by considering the 'e' as x approaches 0:
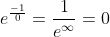
So the functions have equal derivatives as x approaches 0.
Hence the piece-wise function is differentiable as x=0 with the derivative being 0. It then follows that it must be 'k' times differentiable at x=0 with the k'th derivative = 0 for each non-negative integer 'k'.
At x=0, both functions are equal to 0.
(This is an example of a smooth function which is zero and has all derivatives zero at a certain point, but is NOT the zero function.)
Now we show that the derivatives are also equal as the functions approach x=0.
It is trivial that the derivative of 0 is 0 as x approaches 0.
Now
As x approaches 0, the 'e' will dominate the 'x'. So by considering the 'e' as x approaches 0:
So the functions have equal derivatives as x approaches 0.
Hence the piece-wise function is differentiable as x=0 with the derivative being 0. It then follows that it must be 'k' times differentiable at x=0 with the k'th derivative = 0 for each non-negative integer 'k'.


