kingkong123
Member
- Joined
- Dec 20, 2011
- Messages
- 98
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
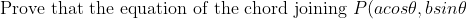 \textup{ and } Q(acos\alpha, bsin\alpha)\textup{ of the ellipse } \\ \frac{x^2}{a^2} + \frac{y^2}{b^2}=1 \textup{ is } bcos\frac{\theta + \alpha}{2}x + asin(\frac{\theta + \alpha}{2})y = abcos(\frac{\theta - \alpha}{2}). )
i did it but i want to know if there's a neater/easier solution.
go wild
i did it but i want to know if there's a neater/easier solution.
go wild
