SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: HSC 2013 4U Marathon
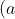 The equation of the ellipse E is$\; \frac{(x-h)^2}{a^2}+\frac{y^2}{b^2}=1\; $where a,b,h are real and a,b is greater than zero.$)
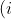 By integration find the area enclosed by E.$)
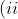 If$\; y=mx \;$is a tangent to$\; E\; $show that$\; m^2=\frac{b^2}{h^2-a^2})
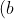 If n belongs to the set of natural numbers, let$ \;E_{n} \;$be the ellipse given by$)
^2}{(a_{n})^2}+\frac{y^2}{p^2(a_{n})^2}=1\; $where$\; p>0, h_{n}>h_{n+1}, h_{n}>a_{n}>0\;)
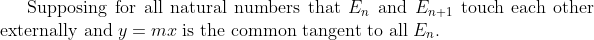
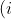 Express$\; h_{n}-h_{n+1} \;$in terms of$\; a_{n}\;$and$\; a_{n+1}.)
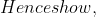
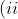$\;\frac{a_{n+1}}{a_{n}}=\frac{h_{1}-a_{1}}{h_{1}+a_{1}})
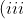$ $If$\; S_{n}\; $is the area enclosed by the ellipse$\; E_{n}. \;$Evaluate$\; \sum_{n=1}^{\infty } S_{n}\; $in terms of$\; a_{1}, h_{1}, p.)
Last edited:
Notice the point (0,0) representing z=0 lies on the circle lz-1l=1, initially we were given (1/z)+(1/conjugate(z))=1 and so z=/=0.
Ahhhhhhhh ok then. Can't believe I fell for that haha, will definitely remember this next time.Yes it is the 'mindless algebra', think carefully about what z can be
I would say:Ahhhhhhhh ok then. Can't believe I fell for that haha, will definitely remember this next time.
So I just have to add z=/=0 at the end right?
By setting a=b=1 your answer has the revolutionary consequence that the unit circle has area 8/3.
Since it is just a translation, I will use "a" and "-a" as my limits of integration. Noting we want area, and the ellipse is symmetrical, I shall use the limits 0 to "a" and multiply by 4. I will also disregard the "-h" due to this translation:
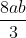
What did I do wrong then? I was typing it up whilst waiting to respawn in a game, so might have made some random error. (or completely fucked up).By setting a=b=1 your answer has the revolutionary consequence that the unit circle has area 8/3.
lol shit, massive fail on my behalf.Square root magically disappeared.
Holes, holes, holesAhhhhhhhh ok then. Can't believe I fell for that haha, will definitely remember this next time.
So I just have to add z=/=0 at the end right?
*sigh*(123)Holes, holes, holes
Not quite. I am not sure how you arrived at your observation in the second line.where
denotes the p'th triangular number.
Note
Noting that
Let's hope I didn't fuck anything up this time.
Yep I'm going to go through and make sure the observations are right, I was just using the identities I found when I used to mess around with triangular numbers, probs got one of them slightly wrong.Not quite. I am not sure how you arrived at your observation in the second line.
I see, well I changed the question so you know if you got it right or not.Yep I'm going to go through and make sure the observations are right, I was just using the identities I found when I used to mess around with triangular numbers, probs got one of them slightly wrong.
Heh, I believe you are over complicating the question a bit. In your original solution you made an observation that you could of just applied into the expression. Apply the given sum and you are done.Ok so far I have:
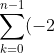^k(n-k)t_{n-k})
So it is obvious how you WANT students to do this question so I won't write that solution up. But just a neat observation, the notion of a sequences "derivative" from http://community.boredofstudies.org/showthread.php?t=292775 can be used to solve this question kind of nicely. It also allows you to generalise the result to an arbitrary number of nested summations!
