RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Dividing by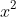 gives:
gives:
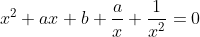
Grouping appropriate terms:
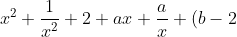 = 0)
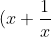^2 + a(x+\frac{1}{x}) + (b-2) = 0)
Now using the quadratic formula:
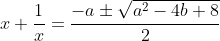
Now let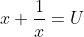
We want to find the values of U such that it has atleast one real root:
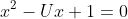
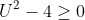
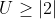
So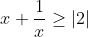
Therefore going back to our quadratic equation and the roots:
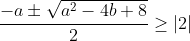
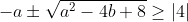
This is where I got up to last time, I'll try again though:bump.
Difficulty: 3.14159/5
That should be enough to keep 2013'ers busy for a while.
Dividing by
Grouping appropriate terms:
Now using the quadratic formula:
Now let
We want to find the values of U such that it has atleast one real root:
So
Therefore going back to our quadratic equation and the roots:
