Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
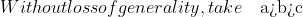
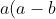(a-c) + b(b-a)(b-c) + c(c-a)(c-b) = )
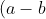(a-c)(b-c) \left(\frac{a}{b-c} - \frac{b}{a-c} + \frac{c}{a-b} \right) )
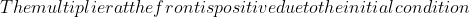
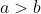
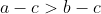
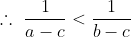
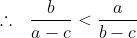
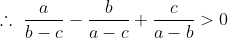
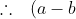(a-c)(b-c) \left(\frac{a}{b-c} - \frac{b}{a-c} + \frac{c}{a-b} \right ) > 0 )
-----
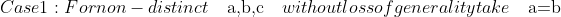
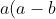(a-c) + b(b-a)(b-c) + c(c-a)(c-b) = c(c-a)^2 > 0 )
(a-c) + b(b-a)(b-c) + c(c-a)(c-b) = 0 )
Hence we account for all cases and inequality holds each time
First, we will prove this is true for distinct a,b,cProve that for all non-negative a,b,c
a(a-b)(a-c)+b(b-a)(b-c)+c(c-a)(c-b) >= 0
-----
Hence we account for all cases and inequality holds each time





