HSC 2015 MX2 Marathon (archive) (6 Viewers)

InteGrand · Oct 4, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
Is i's answer 37 Newtons?

$No, if that were the answer, it would mean that the string isn't even strong enough to simply hold the mass up, assuming we are on Earth (the force required to do this has magnitude $mg=5\times 9.8 = 49$ newtons). The answer is given by $T = m\ell \omega_{\text{max.}}^2$ (see earlier posts), where $\omega_{\text{max.}}=1.5\pi$ rad/s, $\ell = 3$ m, and $m = 5$ kg. So the answer is $T = 5\times 3 \times (1.5\pi)^2 \approx 333$ N.$

asdfghjklqwerty · Oct 4, 2015

Re: HSC 2015 4U Marathon

can someone do part ii please

Paradoxica · Oct 4, 2015

Re: HSC 2015 4U Marathon

asdfghjklqwerty said:
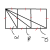
A 3 metre string AB has a mass of 5kg attached at point B. The string is rotated in a horizontal circle about A and breaks as soon as it exceeds a speed of rotation of 45 revolutions per minute.
i.Find the maximum possible tension in the string.
ii. the mass at B is replaced by a 3kg mass and an additional 1kg mass is attached to the string at C, 2 metres from A (as shown below). Find the new maximum number of revolutions per minute that the string can be rotated.

i need help with part ii now ( thanks
ans: 52.5revs/minute

Ohohoho, I remember doing this question. The tension in the second scenario is 11 newtons...

asdfghjklqwerty · Oct 4, 2015

Re: HSC 2015 4U Marathon

can u tell me how to do it??

Paradoxica · Oct 4, 2015

Re: HSC 2015 4U Marathon

I barely understand how forces interact between objects, sorry man. That's just what I got. The tension exerted by the 1 kg mass should be 2 N and the tension exerted by the 3kg mass should be 9 N. You need to use your own understanding of tension to justify that.

Zlatman · Oct 4, 2015

Re: HSC 2015 4U Marathon

$Let the tension at $ C = T_1 $, the tension at $ B = T_2 $ and the total tension in the string $ = T$.$

$Note that the diagram will be two circles with centre A, with C circling with radius 2 and B circling with radius 3.$

$Horizontal component of the forces at C:$
$\begin{align*} T_1 &= mrw^2 \\ &= 1 * 2 * w^2 \\ T_1 &= 2w^2 \end{align*}$

$Horizontal component of the forces at B:$
$\begin{align*} T_2 &= mrw^2 \\ &= 3 * 3 * w^2 \\ T_2 &= 9w^2 \end{align*}$

$\begin{align*}T &= T_1 + T_2 \\ &= 11w^2 \\ \frac{135 \pi^2}{4} &= 11w^2 (*) \\ \frac{135 \pi^2}{44} &= w^2 \\ w &= 5.502 \, radians \, per \, second \\ &= 52.5 \, revolutions \, per \, minute \end{align*}$

(* - max tension from part i)

Sy123 · Oct 4, 2015

Re: HSC 2015 4U Marathon

$\\ $Consider the polynomial$ \ p(x) = x^3 - 3x + 1 \\ \\ $i) Transform the equation into a function of$ \ t \ $using the substitution$ \ x = t + \frac{1}{t} \\ \\ $ii) Hence or otherwise, show that$ \ x = -2\cos \frac{\pi}{9} \ $is a root of the polynomial$ \ p(x)$

Zlatman · Oct 4, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ $Consider the polynomial$ \ p(x) = x^3 - 3x + 1 \\ \\ $i) Transform the equation into a function of$ \ t \ $using the substitution$ \ x = t + \frac{1}{t} \\ \\ $ii) Hence or otherwise, show that$ \ x = -2\cos \frac{\pi}{9} \ $is a root of the polynomial$ \ p(x)$

$P(x) = x^3 - 3x + 1$

$$Substitute $ x = t + \frac{1}{t}$

$\begin{align*} P(t + \frac{1}{t}) &= (t + \frac{1}{t})^3 - 3(t + \frac{1}{t}) + 1 \\ &= t^3 + 1 + \frac{1}{t^3} \end{align*}$

$$Let $t = cis \theta$

$$Therefore, $ \\ \begin{align*} t + \frac{1}{t} &= 2cos \theta \\ x &= 2 cos \theta \end{align*}$

$\begin{align*} When \, x^3 - 3x + 1 &= 0 \\ t^3 + 1 + \frac{1}{t^3} &= 0 \\ t^3 + \frac{1}{t^3} &= -1 \\ 2cos3\theta &= -1 \\ 3\theta &= \frac{2\pi}{3} \, or \, \frac{4\pi}{3} \, or \, \frac{8\pi}{3} \\ \theta &= \frac{2\pi}{9} \, or \, \frac{4\pi}{9} \, or \, \frac{8\pi}{9} \end{align*}$

$Therefore, $ x = 2 cos \frac{8\pi}{9} $ is a root of P(x).$ \\ $i.e. $ x = -2 cos \frac{\pi}{9} $ is a root of P(x).$

kawaiipotato · Oct 6, 2015

Re: HSC 2015 4U Marathon

Find alpha + beta + gamma

All squares are of side lengths 1.
There's a way using complex numbers

InteGrand · Oct 6, 2015

Re: HSC 2015 4U Marathon

kawaiipotato said:
View attachment 32500
Find alpha + beta + gamma

All squares are of side lengths 1.
There's a way using complex numbers

This is a classic problem and has something like 50+ different known solutions iirc. One classic solution is via reflecting the diagram, and is shown in a Numberphile video (linked below). (Can also solve via inverse trig., requires an inverse trig. addition identity).

[video]https://youtube.com/watch?v=m5evLoL0xwg[/video]

psyc1011 · Oct 6, 2015

Re: HSC 2015 4U Marathon

InteGrand said:
This is a classic problem and has something like 50+ different known solutions iirc. One classic solution is via reflecting the diagram, and is shown in a Numberphile video (linked below). (Can also solve via inverse trig., requires an inverse trig. addition identity).

[video]https://youtube.com/watch?v=m5evLoL0xwg[/video]

Geez... such creativity

kawaiipotato · Oct 6, 2015

Re: HSC 2015 4U Marathon

I saw that one and the complex number one which I liked lol. arg((i+1)(i+2)(i+3)) = arg(10i) = pi/2

Drsoccerball · Oct 14, 2015

Re: HSC 2015 4U Marathon

Here's an easy one to kickstart this marathon again:

$Use De moivre's theorem to prove both the sin and cos double angle formulas$

kawaiipotato · Oct 14, 2015

Re: HSC 2015 4U Marathon

$Consider the expression,$

$(\cos \theta + i \sin \theta )^{2}$

$\equiv \cos 2 \theta + i \sin 2 \theta ( $ by De Moivre's Theorem $ )$

$\equiv \cos^{2} \theta - \sin^{2} \theta + 2i \cos \theta \sin \theta$

$Equating real and imaginary parts of both expansions,$

$\cos 2 \theta \equiv \cos^{2} \theta - \sin^{2} \theta$

$\sin 2 \theta \equiv 2 \sin \theta \cos \theta$

$____________________________________________________$

$New question$

$$ Given a^2 + b^2 = c^2 + d^2 = 1$

$$ ac + bd $ = 0$

$What is the value of ab + cd ?$

glittergal96 · Oct 14, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
Here's an easy one to kickstart this marathon again:

$Use De moivre's theorem to prove both the sin and cos double angle formulas$

Lol, De Moivre's theorem is usually proved USING the trig addition formulae. This is quite circular.

braintic · Oct 14, 2015

Re: HSC 2015 4U Marathon

glittergal96 said:
Lol, De Moivre's theorem is usually proved USING the trig addition formulae. This is quite circular.

Only the limited version involving integer powers.

glittergal96 · Oct 14, 2015

Re: HSC 2015 4U Marathon

braintic said:
Only the limited version involving integer powers.

Well when we stop talking about integer power we start getting multivalued.

A full statement of the theorem is then slightly clunkier, but could still be obtained by using the integer power version to obtain the rational power version, and using the continuity of the trig functions to extend this to the reals.

Anyway, this is a digression. The version of De Moivres used in answering this question is only required to treat integer powers, and any proof of this version of De Moivres either explicitly uses the trig addition formulae or proves this fact in disguise.

glittergal96 · Oct 14, 2015

Re: HSC 2015 4U Marathon

kawaiipotato said:
$Consider the expression,$

$(\cos \theta + i \sin \theta )^{2}$

$\equiv \cos 2 \theta + i \sin 2 \theta ( $ by De Moivre's Theorem $ )$

$\equiv \cos^{2} \theta - \sin^{2} \theta + 2i \cos \theta \sin \theta$

$Equating real and imaginary parts of both expansions,$

$\cos 2 \theta \equiv \cos^{2} \theta - \sin^{2} \theta$

$\sin 2 \theta \equiv 2 \sin \theta \cos \theta$

$____________________________________________________$

$New question$

$$ Given a^2 + b^2 = c^2 + d^2 = 1$

$$ ac + bd $ = 0$

$What is the value of ab + cd ?$

I don't think those conditions uniquely determine ab + cd...

Paradoxica · Oct 14, 2015

Re: HSC 2015 4U Marathon

kawaiipotato said:
$Consider the expression,$

$(\cos \theta + i \sin \theta )^{2}$

$\equiv \cos 2 \theta + i \sin 2 \theta ( $ by De Moivre's Theorem $ )$

$\equiv \cos^{2} \theta - \sin^{2} \theta + 2i \cos \theta \sin \theta$

$Equating real and imaginary parts of both expansions,$

$\cos 2 \theta \equiv \cos^{2} \theta - \sin^{2} \theta$

$\sin 2 \theta \equiv 2 \sin \theta \cos \theta$

$____________________________________________________$

$New question$

$$ Given a^2 + b^2 = c^2 + d^2 = 1$

$$ ac + bd $ = 0$

$What is the value of ab + cd ?$

$$Consider $a+bi$ and $c+di$. $|a+bi| = 1, |c-di|= 1, |a+bi||c-di| = 1 \Rightarrow |ac + bd + i(bc - ad)| = 1 \Rightarrow bc-ad = 1$ (actually, ab+cd is multivalued... checked using W|A)

kawaiipotato · Oct 14, 2015

Re: HSC 2015 4U Marathon

glittergal96 said:
I don't think those conditions uniquely determine ab + cd...

There's only one solution for ab + cd

HSC 2015 MX2 Marathon (archive) (6 Viewers)

Well-Known Member

Member

-insert title here-

Member

-insert title here-

Member

This too shall pass

Member

Well-Known Member

Well-Known Member

#truth

Well-Known Member

Well-Known Member

Well-Known Member

Active Member

Well-Known Member

Active Member

Active Member

-insert title here-

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 6)