you mean |x| < 1, negative values of x and zero still work
to make sure the GP converges, do it like this:
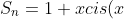+x^2cis(2x)+...+x^ncis(nx) = \frac{1 - (xcisx)^n}{1-xcisx})
So if we let
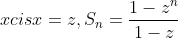
which converges as n->infinity if |z| < 1, and diverges if |z|>1. If |z|=1, i.e. x = 1 or -1, it neither converges nor diverges: it just sorta oscillates around the place (although, since 1 is not a rational multiple of pi, its not actually periodic but rather slightly chaotic). Clearly |z| = |x|, so it converges iff |x|<1, goes weird if |x| = 1 and diverges if |x| > 1.
Cool question!
EDIT: oh wait I kinda messed it up because I showed the cis sum diverges, not Re(cissum). Its pretty easy to do that though I think:
+isin(nx))}{1-x(cosx+isinx)}\right)
= \frac{(1-x^ncos(nx))(1-xcosx)+x^{n+1}sinxsin(nx)}{(1-xcosx)^2+x^2sin^2x}
= \frac{1-xcosx+x^n(xcos((n-1)x)-cos(nx))}{1-2xcosx+x^2})
Now note that as n goes to infinity, the demoninator remains the same while the numerator converges if |x|<1. For |x|>=1, its a lot more complicated but it certainly doesnt converge; it doesnt necessarily "increase without bound though", it sorta oscillates whilst "diverging" at the same time (I dont actually know the technical definition of diverging so yeah, in this case a function like xsinx diverges even though it has zeroes for arbitrarily large x)

