Since this is a multi-part question, we probably need to use one of the previous parts.
From part ii we get that
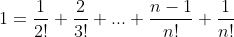
now we need to show that the sum of
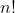
is equal to the sum of n distinct divisors, so we should try to make n! the subject of the equation.
Simply reorganising the equation gives us a very messy answer which probably will not work.
An alternate path would be to multiply both sides by n!. This gives us n! on one side and a series of additions on the other, which is a good sign.
n!}{n!}+1)
and this appears to be the solution, since we have n! in the numerator of every term except the last, all of them will be an integer cause the denominator is in between 2 and n!.
We know that this sequence will have n terms cause the first part of the equation (excluding that +1) will have exactly n-1 terms, hence including the +1 will give n terms.
We also know that this will give us divisors of n! because the denominator will cancel out with the numerator. ie
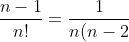!})
which will give a factor of n!
Testing this out for 4!
4!}{4!}+1)
note how there are exactly four terms
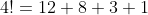
also notice how these are divisors of 24
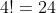
as required
is equal to the sum of n distinct divisors, so we should try to make n! the subject of the equation.
and this appears to be the solution, since we have n! in the numerator of every term except the last, all of them will be an integer cause the denominator is in between 2 and n!.
which will give a factor of n!
note how there are exactly four terms
also notice how these are divisors of 24
as required
