So, in class we came across this problem, and we're still pondering the explanation. Thoughts?
The integral we want to find is that of
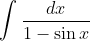
METHOD 1:
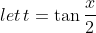
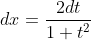
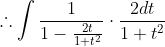
Which simplifies to
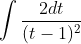
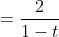
Now I'll leave it in this form for the sake of comparison.
METHOD 2
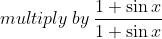
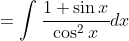
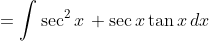
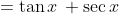
Now substituting in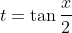
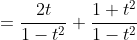
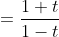
This result is different to what was obtained using the t method formula. Of course, there's an arbitrary constant added, but how can the difference lie in the constant if there's an additional variable of t in the numerator?
The integral we want to find is that of
METHOD 1:
Which simplifies to
Now I'll leave it in this form for the sake of comparison.
METHOD 2
Now substituting in
This result is different to what was obtained using the t method formula. Of course, there's an arbitrary constant added, but how can the difference lie in the constant if there's an additional variable of t in the numerator?
