someone with too much time on their hands can compile it into an actual coroneos style worksheetone day we’re gonna have ‘1000 Proofs’ at this rate
ooh that reminds me - has anyone done steve howard's thousand problems worksheet??? is it any good?
someone with too much time on their hands can compile it into an actual coroneos style worksheetone day we’re gonna have ‘1000 Proofs’ at this rate
very goodsomeone with too much time on their hands can compile it into an actual coroneos style worksheet
ooh that reminds me - has anyone done steve howard's thousand problems worksheet??? is it any good?
With the 2023 HSC we can add these proof questionsMaybe the 2023 HSC exam will make it 400 or near that.
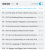
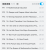

ngl if i'm bored enough one day i mightsomeone with too much time on their hands can compile it into an actual coroneos style worksheet
Here are some more. The last one isn't out yet, but comes out in April.Pólya, G., Mathematics and Plausible Reasoning Vol 1 and 2, Princeton University Press, 1954
Franklin, J.; Daoud, A., Proof in Mathematics: An Introduction, Kew Books, 2011
Gold, Bonnie; Simons, Rogers A.. Proof and Other Dilemmas: Mathematics and Philosophy. MAA., 2008
Solow, D., How to Read and Do Proofs: An Introduction to Mathematical Thought Processes, Wiley, 2004
Velleman, D., How to Prove It: A Structured Approach, Cambridge University, 2006
Hammack, Richard, Book of Proof, 2018
Cupillari, Antonella. The Nuts and Bolts of Proofs: An Introduction to Mathematical Proofs, 4th ed. Academic Press., 2013
The ebook for this last one is now available. It came out a bit early a few hours ago. If you are old fashioned and want a hardcopy version you will still have to wait.......Draganov, A., Taking the “Oof!” Out of Proofs: A Primer on Mathematical Proofs, CRC Press, 2024 (release date April 8, 2024)
you may have to wait a bit longer for the last one.
so how about the biggest proof ever - that every finite simple group is cyclic of prime order, alternating, Lie type or sporadic
- classification of finite simple groups
2023 are there nowhttp://www.westmaths.com.au/home/ from 2018-2022 (the 2023 not there yet)
