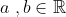This is a lot of working for a relatively easy question. The locus of z is a circle centre 0,0 and radius 2. The locus of bz is a circle centre 0,0 with radius of 2b. The value of a shifts this circle in the real axis. So we have the locus of a+bz with radius 2b and centre at (-a,0) its late so im not sure but im pretty sure thats right.
 , then find the locus of complex number
, then find the locus of complex number )